Cross v.s. Nested and Lmer()
Cross v.s. Nested
Introduction
A more general definition of crossed random effects is simply: not nested.
First note that:
- Nesting is a property of the data, or rather the experimental design, not the model.
嵌套是数据的属性,或者说是实验设计的属性,而不是模型的属性。
- Nested data can be encoded in at least 2 different ways, and this is at the heart of the issue you found. Nested数据可以以至少2种方式编码。
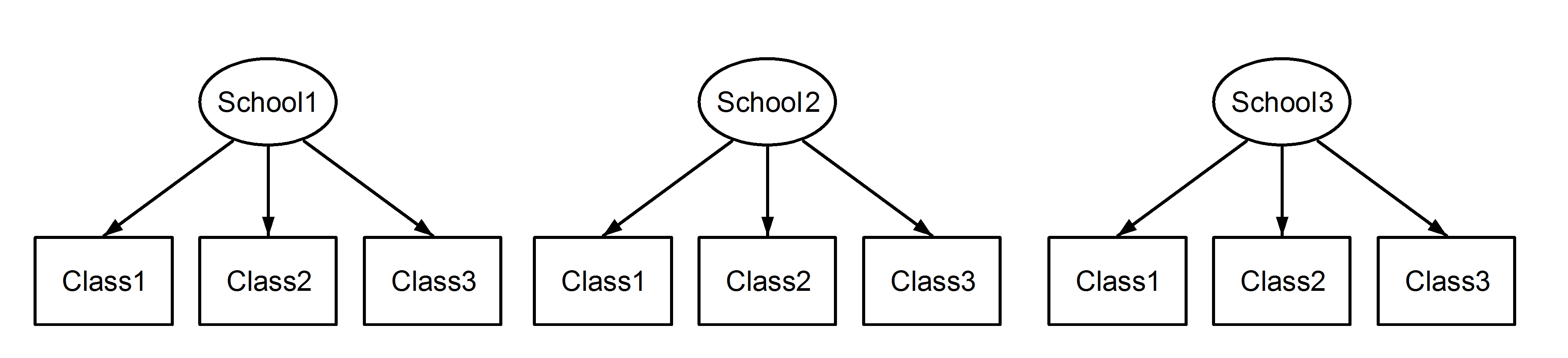
每一个教室都nested in学校,重要的是,每个学校之间,教室都有相同的标识, even though they are distinct if they are nested. Class1 appears in School1, School2 and School3.
However if the data are nested then Class1 in School1 is not the same unit of measurement as Class1 in School2 and School3. If they were the same, then we would have this situation:
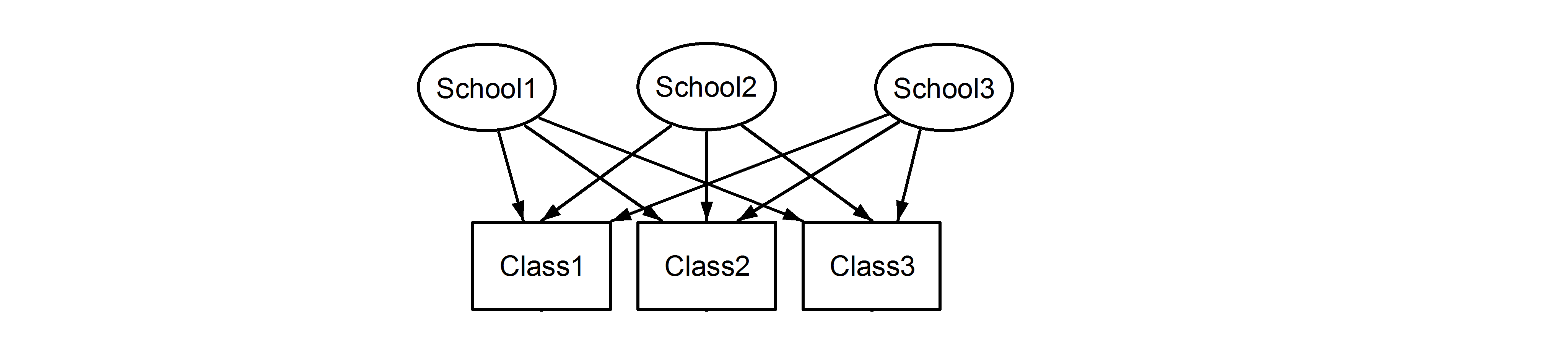
which means that every class belongs to every school. The former is a nested design, and the latter is a crossed design and we would formulate these in lme4 using:1
(1|School/Class) # nested
and1
(1|School) + (1|Class) # cross
由于随机效果是嵌套还是交叉的不确定性,正确指定模型非常重要,因为这些模型将产生不同的结果,如下所示。此外,仅通过检查数据是不可能知道我们是否嵌套了随机效应还是交叉了随机效应。这只能通过数据和实验设计的知识来确定。
考虑一个 case where the Class variable is coded uniquely across schools:

上面这种情况就不再有任何关于嵌套或交叉的歧义了,因为class都有唯一的标识,很明显是nested的特性。 The nesting is explicit(显式). 下面R例子里我们有 6 schools (labelled I-VI) and 4 classes within each school (labelled a to d):1
2
3
4
5
6
7
8
9
10
11
12
13
14
15> dt <- read.table("http://bayes.acs.unt.edu:8083/BayesContent/class/Jon/R_SC/Module9/lmm.data.txt",
header=TRUE, sep=",", na.strings="NA", dec=".", strip.white=TRUE)
> # data was previously publicly available from
> # http://researchsupport.unt.edu/class/Jon/R_SC/Module9/lmm.data.txt
> # but the link is now broken
> xtabs(~ school + class, dt)
class
school a b c d
I 50 50 50 50
II 50 50 50 50
III 50 50 50 50
IV 50 50 50 50
V 50 50 50 50
VI 50 50 50 50
从这个交叉表中我们可以看出,每一个班级的ID都出现在每一所学校下面,这就满足了你对交叉(cross)随机效应的定义 (in this case we have fully, as opposed to partially, crossed random effects, because every class occurs in every school). 这和上面第一幅图中的情况是一样的。然而,如果数据确实是嵌套的而不是交叉的,那么我们需要显式地告诉 lme4:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35# nested
> m0 <- lmer(extro ~ open + agree + social + (1 | school/class), data = dt)
> summary(m0)
Random effects:
Groups Name Variance Std.Dev.
class:school (Intercept) 8.2043 2.8643
school (Intercept) 93.8421 9.6872
Residual 0.9684 0.9841
Number of obs: 1200, groups: class:school, 24; school, 6
Fixed effects:
Estimate Std. Error t value
(Intercept) 60.2378227 4.0117909 15.015
open 0.0061065 0.0049636 1.230
agree -0.0076659 0.0056986 -1.345
social 0.0005404 0.0018524 0.292
# cross
> m1 <- lmer(extro ~ open + agree + social + (1 | school) + (1 |class), data = dt)
> summary(m1)
Random effects:
Groups Name Variance Std.Dev.
school (Intercept) 95.887 9.792
class (Intercept) 5.790 2.406
Residual 2.787 1.669
Number of obs: 1200, groups: school, 6; class, 4
Fixed effects:
Estimate Std. Error t value
(Intercept) 60.198841 4.212974 14.289
open 0.010834 0.008349 1.298
agree -0.005420 0.009605 -0.564
social -0.001762 0.003107 -0.567
答案明显不同因为 m0 is a nested model while m1 is a crossed model.
现在,如果我们为class标识引入一个新变量:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20> dt$classID <- paste(dt$school, dt$class, sep=".")
> xtabs(~ school + classID, dt)
classID
school I.a I.b I.c I.d II.a II.b II.c II.d III.a III.b III.c III.d IV.a IV.b
I 50 50 50 50 0 0 0 0 0 0 0 0 0 0
II 0 0 0 0 50 50 50 50 0 0 0 0 0 0
III 0 0 0 0 0 0 0 0 50 50 50 50 0 0
IV 0 0 0 0 0 0 0 0 0 0 0 0 50 50
V 0 0 0 0 0 0 0 0 0 0 0 0 0 0
VI 0 0 0 0 0 0 0 0 0 0 0 0 0 0
classID
school IV.c IV.d V.a V.b V.c V.d VI.a VI.b VI.c VI.d
I 0 0 0 0 0 0 0 0 0 0
II 0 0 0 0 0 0 0 0 0 0
III 0 0 0 0 0 0 0 0 0 0
IV 50 50 0 0 0 0 0 0 0 0
V 0 0 50 50 50 50 0 0 0 0
VI 0 0 0 0 0 0 50 50 50 50
交叉表显示,按照嵌套的定义,每个级别的类只出现在一个级别的学校中。您的数据也是如此,但是由于数据非常稀疏,因此很难用数据来表示。两个模型公式现在将产生相同的输出 (that of the nested model m0 above):1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33> m2 <- lmer(extro ~ open + agree + social + (1 | school/classID), data = dt)
> summary(m2)
Random effects:
Groups Name Variance Std.Dev.
classID:school (Intercept) 8.2043 2.8643
school (Intercept) 93.8419 9.6872
Residual 0.9684 0.9841
Number of obs: 1200, groups: classID:school, 24; school, 6
Fixed effects:
Estimate Std. Error t value
(Intercept) 60.2378227 4.0117882 15.015
open 0.0061065 0.0049636 1.230
agree -0.0076659 0.0056986 -1.345
social 0.0005404 0.0018524 0.292
> m3 <- lmer(extro ~ open + agree + social + (1 | school) + (1 |classID), data = dt)
> summary(m3)
Random effects:
Groups Name Variance Std.Dev.
classID (Intercept) 8.2043 2.8643
school (Intercept) 93.8419 9.6872
Residual 0.9684 0.9841
Number of obs: 1200, groups: classID, 24; school, 6
Fixed effects:
Estimate Std. Error t value
(Intercept) 60.2378227 4.0117882 15.015
open 0.0061065 0.0049636 1.230
agree -0.0076659 0.0056986 -1.345
social 0.0005404 0.0018524 0.292
It is worth noting that crossed random effects do not have to occur within the same factor. 例如,按照学校的情况,如果我们有 pupils within schools, 而且我们也对学生注册的医生感兴趣,那么我们也会有nesting of pupils within doctors. 这种情况下,学生嵌套于学校下,学生嵌套于医生下,但是医生和学校之间没有嵌套,反之亦然,所以这也是交叉随机效应的一个例子,我们说学校和医生是交叉的。
交叉随机效应发生的类似场景是,单个观察同时嵌套在两个因素中,这通常发生在所谓的重复度量subject-item数据中。通常每个受试者都要用不同的项目进行多次测量/测试,这些相同的项目由不同的受试者进行测量/测试。因此, 观测值 are clustered within 受试者 and within 项目, but 项目 are not nested within 受试者 or vice-versa. Again, we say that subjects and items are crossed.
Summary
交叉随机效应和嵌套随机效应的区别在于,嵌套随机效应发生在一个因素(分组变量)只出现在另一个因素(分组变量)的特定级别时。 This is specified in lme4 with:1
(1|group1/group2)
where group2 is nested within group1.
交叉随机效应更简单了: not nested. This can occur with three or more grouping variables (factors) where one factor is separately nested in both of the others, or with two or more factors where individual observations are nested separately within the two factors. These are specified in lme4 with:1
(1|group1) + (1|group2)
反正可以画出最上面那两个图来看,若是随便交叉都可以的那就是cross了
How to specify random effect terms in lmer() in R
Fixed effects:practice, context and the interaction between the two
Random effects: differ between the models.
Model 1
1 | lmer(ERPindex ~ practice*context + (1|participants), data=base) |
contains a random intercept shared by individuals that have the same value for participants. That is, each participant's regression line is shifted up/down by a random amount with mean 0. Because we assume that participant \(\sim N(0,\sigma^2)\).
Model 2
1 | lmer(ERPindex ~ practice*context + (1+practice|participants), data=base) |
This model, in addition to a random intercept, also contains a random slope in practice. This means that the rate at which individuals learn from practice is different from person to person.
If an individual has a positive random effect, then they increase more quickly with practice than the average, while a negative random effect indicates they learn less quickly with practice than the average, or possibly get worse with practice, depending on the variance of the random effect (this is assuming the fixed effect of practice is positive).
Model 3
1 | lmer(ERPindex ~ practice*context + (practice|participants) + |
This model fits a random slope and intercept in practice (you have to do (practice-1|...) to suppress the intercept), just as the previous model did, but now you've also added a random slope and intercept in the factorparticipants:context, which is a new factor whose levels are every combination of the levels present in participants and context and the corresponding random effects are shared by observations that have the same value of both participants and context. To fit this model you will need to have multiple observations that have the same values for both participants and context or else the model is not estimable. In many situations, the groups created by this interaction variable are very sparse and result in very noisy/difficult to fit random effects models, so you want to be careful when using an interaction factor as a grouping variable.
Basically (read: without getting too complicated) random effects should be used when you think that the grouping variables define "pockets" of inhomogeneity in the data set or that individuals which share the level of the grouping factor should be correlated with each other (while individuals that do not should not be correlated) - the random effects accomplish this. If you think observations which share levels of both participants and context are more similar than the sum of the two parts then including the "interaction" random effect may be appropriate.
Correlated / Uncorrelated Slope and Intercept
Edit: As @Henrik mentions in the comments, the models you fit, e.g.:1
lmer(ERPindex ~ practice*context + (1+practice|participants), data=base)
make it so that the random slope and random intercept are correlated with each other, and that correlation is estimated by the model. To constrain the model so that the random slope and random intercept are uncorrelated (and therefore independent, since they are normally distributed), you'd instead fit the model:1
2lmer(ERPindex ~ practice*context + (1|participants) + (practice-1|participants),
data=base)
The choice between these two should be based on whether you think, for example, participants with a higher baseline than average (i.e. a positive random intercept) are also likely to have a higher rate of change than average (i.e. positive random slope). If so, you'd allow the two to be correlated whereas if not, you'd constrain them to be independent. (Again, this example assumes the fixed effect slope is positive).