A Simulated Phase II Single Arm Design (ORR as Primary Endpoint)
It is a dummy Phase II single-arm study using ORR (binary endpoint) as primary endpoint. The purpose of this post is to illustrate the theory of Predictive Probability (Lee, J. J., & Liu, D. D. (2008)).
Methods
Calculating predictive probabilities via simulation
Predictive Probability (PP) of Success
Definition: The probability of achieving a successful (significant) result at a future analysis, given the current interim data;
Obtained by integrating the data likelihood over the posterior distribution (i.e. we integrate over future possible responses) and predicting the future outcome of the trial;
Efficacy rules can be based either on Bayesian posterior distributions (fully Bayesian) or frequentist p-values (mixed Bayesian-frequentist)
Description of algorithm
- A phase II study is designed to test: \[ H_0: p \le p_0 \] \[ H_1: p \ge p_1 \] The Type I & II error are defined as \[ P(RejectH_0 \mid H_0) \le \alpha \]
\[ P(NotRejectH_0 \mid H_1)\le \beta \]
Set a maximum accrual of patients to \(N_{max}\)
Assume the prior distribution of response rate \(p\) follows a beta distribution \[ beta(a_0,b_0) \] Assume the responders in the current \(n(n<N_{max})\), \(X\), follows a binomial distribution \(Bin(n,p)\);
Based on this the posterior distribution of the \(p\) follows a beta distribution (\(x\) is the observed responders) \[ p\mid x \sim beta(a_0+x,b_0+n-x) \] Thus, the number of responders in the potential \(m=N_{max}-n\) future patients, \(Y\) follows a beta-binomial distribution \[ Y=i \sim BetaBinomial(m,a_0+x,b_0+n-x) \]
The posterior of \(p\) given \(X=x\) and \(Y=i\) is \[ p \mid X=x,Y=i \sim beta(a_0+x+i,b_0+N_{max}-x-i) \]
Define the probability that the response rate is larger than \(p_0\) given \(X=x\) in the the current stage data (\(n\) patients) and \(Y=i\) in the future \(m\) patients; \[ B_i=P(p>p_0 \mid X=x,Y=i) \]
Comparing \(B_i\) to a threshold \(\theta_T\) yields an indicator \(I_i\) for the efficacious at the end of the trial given the current data \(X=x\) and potential future outcome \(Y=i\) \[ I_{(B_i>\theta_T)} \]
Compute the Predictive Probability (PP) \[ PP=\sum_{i=0}^{m}\left\{Prob ( Y=i \mid x ) \times I_{(B_i>\theta_T)}\right\} \]
Based on the PP given in the below tables, we could decide whether the trial should be stopped if PP is sufficiently low.
In the work of Lee, J. J., Liu, D. D. (2008), a high PP means that the treatment is likely to be efficacious by the end of the study, given the current data, whereas a low PP suggests that the treatment may not have sufficient activity.
Typically, we choose \(\theta_L\) as a small positive number and \(\theta_U\) as a large positive constant, both between 0 and 1 (inclusive).
- If \(PP<\theta_L\), then stop the trial and reject the alternative hypothesis (futility);
- If \(PP>\theta_U\), then stop the trial and reject the null hypothesis (efficacious);
- Otherwise, continue to the next stage until reaching the total sample size.
Type I/II error and power calculation using simulation methods
The phase II study is designed to test: \[ H_0: p \le p_0 \]
\[ H_1: p \ge p_1 \]
The Type I & II error are defined as
\[ P(RejectH_0 \mid H_0) \le \alpha \]
\[ P(NotRejectH_0 \mid H_1)\le \beta \] \[ Power=1-\beta \]
The general view of testing the operating characteristics of a design using PP methods via simulations is (suppose a 2-stage design):
- Set parameters for design
- Under \(H_0\) (\(p \le p_0\)), the Type I error is \(P(\) Accept new treatment \(\mid H_0)\), which is
- success in 1st interim analysis and final analysis: \(PP>\theta_L\) in 1st interim analysis \(\rightarrow\) go to final analysis \(\rightarrow\) success in final analysis
- Under \(H_1\) (\(p \ge p_1\)), the Type II error is \(P(\) Reject new treatment \(\mid H_1)\), which is
- fail in 1st interim analysis or success in 1st interim analysis but fail in final analysis:
- \(PP<=\theta_L\) in 1st interim analysis, stop; or
- \(PP>\theta_L\) in 1st interim analysis \(\rightarrow\) go to final analysis \(\rightarrow\) fail in final analysis (total responders in final analysis \(<r\) (Lee, J. J., Liu, D. D. (2008)))
The function for assessing the operating characteristics of a 2-stage design via simulation is provided as:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55OC <- function(numrep,a0,b0,p0,p1,r,n1,ntotal,thetat,thetal){
alpha <- rep(0, numrep)
beta <- rep(0, numrep)
et <- rep(0, numrep)
for (rep in (1:numrep)) {
v1 <- rbinom(n = n1, size = 1, prob = p0)
v2 <- rbinom(n = ntotal - n1,size = 1,prob = p0)
betav1 <- rbinom(n = n1, size = 1, prob = p1)
betav2 <- rbinom(n = ntotal - n1,size = 1,prob = p1)
sumv1 <- sum(v1)
sumv2 <- sum(v2)
betasumv1 <- sum(betav1)
betasumv2 <- sum(betav2)
pp <-
PredP(
x = sumv1,
n = n1,
nmax = ntotal,
a = a0,
b = b0,
p0 = p0,
theta_t = thetat
)
ppbeta <-
PredP(
x = betasumv1,
n = n1,
nmax = ntotal,
a = a0,
b = b0,
p0 = p0,
theta_t = thetat
)
if (pp >= thetal) {
totalr <- sumv2 + sumv1
rlogic <- totalr > r
alpha[rep] <- TRUE * rlogic
} else {
et[rep] <- TRUE
}
if (ppbeta >= thetal) {
betatotalr <- betasumv2 + betasumv1
betarlogic <- betatotalr <= r
beta[rep] <- TRUE * betarlogic
} else {
beta[rep] <- TRUE
}
}
# cat("early stopping is:", mean(et), "\n")
# cat("type i error:", mean(alpha), "\n")
# cat("type ii error:", mean(beta), "\n")
# cat("power:", 1 - mean(beta))
final <- c(mean(alpha),mean(beta))
return(final)
}
The function for assessing the Type I error of a 3-stage design via simulation is provided as:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39ThreeStageOC <- function(numrep,a0,b0,p0,p1,r,n1,n2,n3,ntotal,thetat,thetal){
alpha <- rep(0, numrep)
for (rep in (1:numrep)) {
v1 <- rbinom(n = n1, size = 1, prob = p0)
v2 <- rbinom(n = n2, size = 1, prob = p0)
v3 <- rbinom(n = ntotal - n1 - n2,size = 1,prob = p0)
sumv1 <- sum(v1)
sumv2 <- sum(v2)
sumv3 <- sum(v3)
pp1 <-
PredP(
x = sumv1,
n = n1,
nmax = ntotal,
a = a0,
b = b0,
p0 = p0,
theta_t = thetat
)
pp2 <-
PredP(
x = sumv1+sumv2,
n = n1+n2,
nmax = ntotal,
a = a0,
b = b0,
p0 = p0,
theta_t = thetat
)
if (pp1 >= thetal) {
if (pp2 >= thetal){
totalr <- sumv3 + sumv2 + sumv1
rlogic <- totalr > r
alpha[rep] <- TRUE * rlogic
}
}
}
cat("type i error:", mean(alpha), "\n")
}
Scenario 1
Objective
To determine the expected sample size and target responders
Parameters
- Set a target response rate for simulate purpose (need medical input)
1 | psim <- 0.3 |
- 1st stage total subjects (we assume this is a point we will look at)
1 | n1 <- 10 |
- Total sample size (we assume this is pre-specified prior to the beginning of trial)
1 | ss <- 36 |
- Success criteria
- Pre-specified response rate for standard treatment: \(p_0=0.3\) (need medical input)
- Pre-specified response rate for new treatment: \(p_1=0.5\) (need medical input if Type II error rate and Power are needed to be evaluated)
- Threshold for considering the treatment is efficacious at the end of the trial given the current data and the potential outcome of future responders (\(I_{(B_i>\theta_T)}\) in the above): \(\theta_T=0.8\) (need medical input)
- The boundary for stopping the trial and reject the alternative hypothesis for futility (cutoff of the predictive probability to indicate unfavorable likelihood for success): \(\theta_L=0.1\) (need medical input)
1 | p_0 <- 0.2 |
- Prior hyper-parameters
The response rate \(p\) follows a beta distribution \(Beta(a_0,b_0)\) (medical should input the response rate estimate) where1
2
3
4
5
6a0 <- 0.2
b0 <- 0.8
# define range for plot
p = seq(0,1, length=100)
# create plot of Beta distribution with shape parameters a0 and b0
plot(p, dbeta(p, a0, b0), type='l')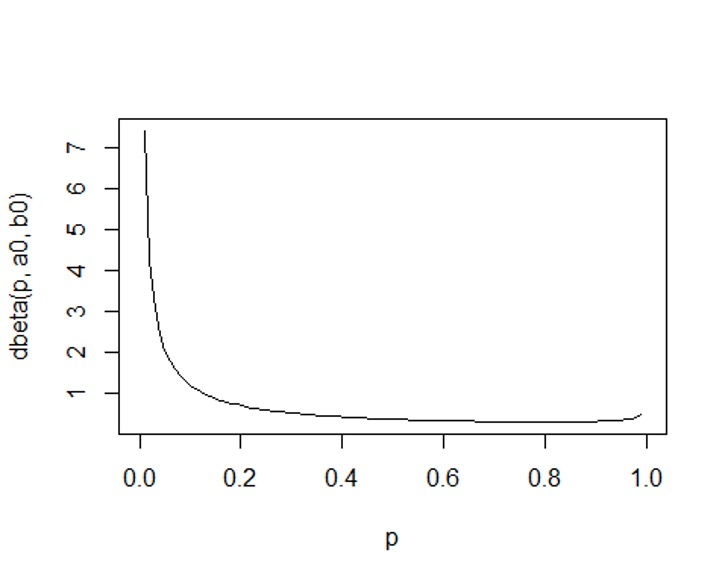
Simulation Code & Results
1 | # call library ph2bye |
1 | #Lee and Liu's criterion function for determining the trial decision cutoffs based on the predictive probability |
General considerations for PP
Note that in the following tables, column "responders" means that the number of observed responders in 1st stage during the trial.
Total sample size of 36 patients enrolled in the first stage.
0. simulate analysis dataset
1 | set.seed(2022) |
Table 1: simulated dataset for stage 1
| subjid | datetime | response |
|---|---|---|
| 1001 | 2022-01-29 | 1 |
| 1002 | 2022-01-29 | 0 |
| 1003 | 2022-01-29 | 0 |
| 1004 | 2022-01-29 | 0 |
| 1005 | 2022-01-29 | 0 |
| 1006 | 2022-01-29 | 0 |
| 1007 | 2022-01-29 | 0 |
| 1008 | 2022-01-29 | 0 |
| 1009 | 2022-01-29 | 0 |
| 1010 | 2022-01-29 | 1 |
Find the target number of responders during the trial
calculate minimum k (Chen DT, et al (2019))
With the assumptions above, we need to calculate the minimum of responders \(k\) needed at the end of trial to claim efficacy by comparing the posterior probability of response rate \(p\) and threshold \(\theta_T\), given \(p_0\):
\[ \textrm{arg min}_Q\textrm{ }k:=\{k, \textrm{for } Q(x)=\int_{p_0}^{1}\left[\frac{1}{B(a_0,b_0)}x^{a_0+k-1}(1-x)^{b_0+N_{max}-k-1}-\theta_T>0 \right] \} \] Based on the current information, we can calculate the expected minimum \(k\) responders needed at the end of trial to claim efficacy:1
2
3
4
5
6
7
8for (k in 1:(ss-1)){
pminik <- beta(a0,b0)*(pbeta(1,a0+k,b0+ss-k)-pbeta(p_0,a0+k,b0+ss-k))-thetat
if (pminik>0){
cat("The expected minimum responders needed at the end of trial to claim efficacy is:",k)
minik<- k
break
}
}
## The expected minimum responders needed at the end of trial to claim efficacy is: 6
*calculate target responders \(r\) (Lee, J. J., Liu, D. D. (2008))
Given the parameters - Total sample size: ss - Prior hyper-parameters: a0, b0 - Response rate for the standard drug under null hypothesis: p0 - Cutoff probability for efficacy including future patients: thetat - Cutoff probability for futility based on PP: thetal
We can search the target responders (or rejection region) based on a given total sample size.1
2
3
4
5
6
7
8
9
10
11DesignA <- PredP.design(type = "futility", nmax=ss, a=a0, b=b0, p0=p_0, theta_t=thetat ,theta=thetal)
DesignAhux <- as_hux(DesignA)
DesignAhux %>%
set_all_padding(4) %>%
set_outer_padding(0) %>%
set_font_size(9) %>%
set_bold(row = 1, col = everywhere) %>%
set_bottom_border(row = 1, col = everywhere) %>%
set_width(0.4) %>%
set_caption("boundary")
Table 2: boundary
| n | bound |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | 0 |
| 11 | 0 |
| 12 | 0 |
| 13 | 0 |
| 14 | 0 |
| 15 | 0 |
| 16 | 0 |
| 17 | 1 |
| 18 | 1 |
| 19 | 1 |
| 20 | 1 |
| 21 | 2 |
| 22 | 2 |
| 23 | 2 |
| 24 | 3 |
| 25 | 3 |
| 26 | 3 |
| 27 | 4 |
| 28 | 4 |
| 29 | 5 |
| 30 | 5 |
| 31 | 6 |
| 32 | 6 |
| 33 | 7 |
| 34 | 8 |
| 35 | 9 |
| 36 | 10 |
From the above report, 10/36 (responders/Total patients) is the rejection region. Since when we observe \(\le 10\) responders in total 36 patients, the PP will be 0:1
PredP(x=10, n=36, nmax=36, a=a0, b=b0, p0=p_0, theta_t=thetat)
Therefore, the number of target responders with this sample size should be \(\ge 11\).1
PredP(x=11, n=36, nmax=36, a=a0, b=b0, p0=p_0, theta_t=thetat)
Note
In the algorithm (Lee, J. J., Liu, D. D. (2008)), we should search thetat and thetal to satisfy the constraints of Type I and Type II error rates.
consider a 2-stage design
Consider a design with 2 planned interim analyses with 10 \(\rightarrow\) 20 patients in the 1st, and final stage. Given we need to search thetal and thetat.
As an example, we will stop the searching when the thetal and thetat satisfy the constraints Type I error rates \(\le 0.10\) and Type II error rate \(\le 0.10\) (just for illustration).1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40gridThetat <- seq(0.860,0.900,0.001)
gridThetal <- seq(0.001,0.010,0.001)
numrep <- 5000
stop <- FALSE
for (i in 1:length(gridThetat)) {
for (j in 1:length(gridThetal)) {
oseva <-
OC(
numrep = numrep,
a0 = a0,
b0 = b0,
p0 = p_0,
p1 = p_1,
r = 10,
n1 = n1,
ntotal = ss,
thetat = gridThetat[i],
thetal = gridThetal[j]
)
# ??? is it correct?
pp <- PredP(x=11, n=36, nmax=36, a=a0, b=b0, p0=p_0, theta_t=gridThetat[i])
# constraints: alpha <= 0.10 and beta <= 0.10
if ((oseva[1] <= 0.10) && (oseva[2] <= 0.10) && (pp>=1)) {
stop <- TRUE
thetat1 <- gridThetat[i]
thetal1 <- gridThetal[j]
break
} else {
next
}
}
if (stop == TRUE) {
break
}
}
cat("theta_t should be: ", thetat1, "\n")
cat("theta_l should be: ", thetal1)
## theta_t should be: 0.86
## theta_l should be: 0.001
Then we can use these two parameters for further analysis.1
2
3# reset parameters for the following formal analysis
thetal <- 0.001
thetat <- 0.86
simulate the number of patients with response in the 1st interim analysis with 10 patients
We list the predictivity probability for all scenarios of number of responders in the first 10 patients (1st interim analysis) and number of responders needed in the remaining \(36-10=26\) patients to have at least a total of \(r=11\) responders (Lee, J. J., Liu, D. D. (2008)).1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20result <-
ppfunc(
mink = 11, # target number of responders
n1 = n1,
nmax = 36,
a0 = a0,
b0 = b0,
p0 = p_0,
thetat = thetat
)
resulthux <- as_hux(result)
resulthux %>%
set_all_padding(4) %>%
set_outer_padding(0) %>%
set_font_size(9) %>%
set_bold(row = 1, col = everywhere) %>%
set_bottom_border(row = 1, col = everywhere) %>%
set_width(0.4) %>%
set_caption("predictive probability based on the results of stage 1") %>%
set_text_color(row = 4, value = "red")
Table 3: predictive probability based on the results of stage 1
| totalsample | responders | pp |
|---|---|---|
| 36 | 0 | 0.000756 |
| 36 | 1 | 0.0311 |
| 36 | 2 | 0.177 |
| 36 | 3 | 0.468 |
| 36 | 4 | 0.766 |
| 36 | 5 | 0.936 |
| 36 | 6 | 0.99 |
| 36 | 7 | 0.999 |
| 36 | 8 | 1 |
| 36 | 9 | 1 |
| 36 | 10 | 1 |
The plot is1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16x_axis_labels <- 0:10
p <-
ggplot(data = result, aes(
x = responders,
y = pp
)) +
geom_bar(stat = "identity", fill = "steelblue", width = 0.5) +
labs(title = "Simulation for 1st interim analysis", x = "#responders in the 1st interim analysis with 10 patients", y = "Predictive probability") +
geom_text(aes(label = sprintf("%0.2f", pp)),
vjust = 1.6,
color = "black",
size = 3) +
scale_x_continuous(labels = x_axis_labels, breaks = x_axis_labels)+
geom_hline(yintercept=thetal, linetype="dashed", color = "red", size=1)+
theme_minimal()
p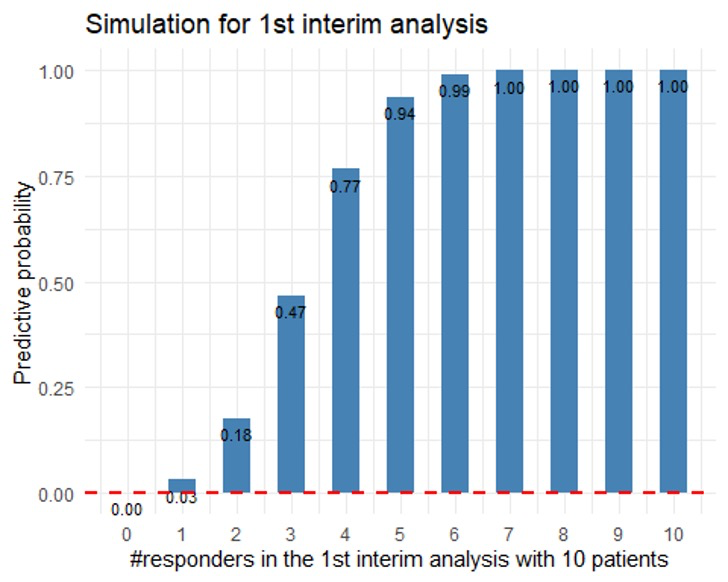
Since we observe 2 responders in the 1st interim analysis, we can go to next stage.
simulate the number of patients with response in the final analysis with 26 patients
1 | # create the analysis data set for stage II |
## Number of responders in stage 2: 12
Table 4: simulated dataset for stage 2
| subjid | datetime | response |
|---|---|---|
| 1011 | 2022-03-29 | 1 |
| 1012 | 2022-03-29 | 0 |
| 1013 | 2022-03-29 | 0 |
| 1014 | 2022-03-29 | 0 |
| 1015 | 2022-03-29 | 0 |
| 1016 | 2022-03-29 | 0 |
| 1017 | 2022-03-29 | 1 |
| 1018 | 2022-03-29 | 0 |
| 1019 | 2022-03-29 | 0 |
| 1020 | 2022-03-29 | 1 |
| 1021 | 2022-03-29 | 1 |
| 1022 | 2022-03-29 | 0 |
| 1023 | 2022-03-29 | 0 |
| 1024 | 2022-03-29 | 0 |
| 1025 | 2022-03-29 | 0 |
| 1026 | 2022-03-29 | 1 |
| 1027 | 2022-03-29 | 1 |
| 1028 | 2022-03-29 | 0 |
| 1029 | 2022-03-29 | 1 |
| 1030 | 2022-03-29 | 1 |
| 1031 | 2022-03-29 | 1 |
| 1032 | 2022-03-29 | 1 |
| 1033 | 2022-03-29 | 1 |
| 1034 | 2022-03-29 | 0 |
| 1035 | 2022-03-29 | 1 |
| 1036 | 2022-03-29 | 0 |
Based on the 12 responders, we have total 14 responders in the trial which is larger than 10.
We will consider the new treatment since it warrants further development.
Discussion
Given total sample size, varing responders \(r\) to search \(\theta_t\) and \(\theta_l\)
Suppose total sample size is still 36, we vary the number of responders \(r\) from 6 to 15 to find the combination of \(r\), \(\theta_t\) and \(\theta_l\) satisfying the constraints of Type I and Type II error rates.
The results are given in the Appendix B.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84# set the constaints for Type I/II error rates
typei <- 0.05
typeii <- 0.20
# the range of parameters
gridr <- seq(6,15,1)
gridThetal <- seq(0.001,0.03,0.001)
gridThetat <- seq(0.70,0.95,0.001)
numrep <- 4000
# function to search the combination of parameters
searchPara <-
function(gridr,
gridThetat,
gridThetal,
nmax,
n1,
a,
b,
p0,
p1,
repnum,
alpha,
beta) {
mat <- matrix(NA, 1000, 6)
rowindex <- 1
for (r in gridr) {
for (i in 1:length(gridThetat)) {
for (j in 1:length(gridThetal)) {
rejreg <-
PredP.design(
type = "futility",
nmax = nmax,
a = a,
b = b,
p0 = p0,
theta = gridThetal[j]
)
rejbound <- tail(rejreg$bound, n = 1)
if (!(rejbound == r)) {
break
} else {
oseva <-
OC(
numrep = numrep,
a0 = a,
b0 = b,
p0 = p0,
p1 = p1,
r = r + 1,
n1 = n1,
ntotal = nmax,
thetat = gridThetat[i],
thetal = gridThetal[j]
)
# constraints: alpha <= 0.10 and beta <= 0.10
if ((oseva[1] <= alpha) && (oseva[2] <= beta) && (rowindex <= 1000)) {
stop <- TRUE
thetat1 <- gridThetat[i]
thetal1 <- gridThetal[j]
mat[rowindex, 1] <- nmax
mat[rowindex, 2] <- r
mat[rowindex, 3] <- thetat1
mat[rowindex, 4] <- thetal1
mat[rowindex, 5] <- oseva[1]
mat[rowindex, 6] <- oseva[2]
rowindex <- rowindex + 1
break
}
}
}
if (stop == TRUE) {next}
}
}
df <- data.frame(mat)
colnames(df) <- c("N","r","theta_t","theta_l","Type_I","Type_II")
df <- df[complete.cases(df), ]
return(df)
}
The choice of parameters for beta prior
Information about response data of the experimental treatment helps determine the beta prior distribution, \(beta(a,b)\), for the response rate where
- \(a\) represents the degree of response (e.g., number of responders)
- \(b\) indicates magnitude of non-response (e.g., number of non-responders).
The mean response rate is \(a/(a+b)\) with
- \(a>b\) for tendency of more drug-sensitive
- \(a<b\) for more drug-resistant
- \(a=b\) for undetermined.
In addition, when \(a+b\) becomes large, the belief of prior information gets strong and likely dominates the result.
While many experimental treatments are usually the first study, some of them are a combination of standard treatment with new drug or modification of standard treatment. Thus, utilization of historical data could help better shape prior distribution within the Bayesian framework.
Often prior information provided by a physician is not the values of \(a\) and \(b\), but a response rate estimate. Conversion to the two parameters (\(a\) and \(b\)) can be done by a formula with a hypothesized standard deviation (SD) of response rate (\(p\)): \[ p=\frac{a}{a+b} \]
\[ a = \left(\frac{1-p}{SD^2}-\frac{1}{p} \right)p^2 \]
\[ b = a \left(\frac{1}{p}-1 \right) \]
Minimally informative prior distribution
Minimally informative (less direct but synonymous terms are diffuse, weak, and vague) priors fall into two broad classes:
so-called non-informative priors, which attempt to be completely objective, in that the posterior distribution is determined as completely as possible by the observed data, the most well known example in this class being the Jeffreys prior (for beta distribution it's \(Beta(0.5,0.5)\)), and
priors that are diffuse over the region where the likelihood function is non-negligible, but that incorporate some information about the parameters being estimated, such as a mean value.
In contrast, the use of informative prior distributions explicitly acknowledges that the analysis is based on more than the immediate data in hand whose relevance to the parameters of interest is modelled through the likelihood, and also includes a considered judgement concerning plausible values of the parameters based on external information.
In fact the division between these two options is not so clear-cut — in particular, we would claim that any “objective” Bayesian analysis is a lot more “subjective” than it may wish to appear.
- First, any statistical model (Bayesian or otherwise) requires qualitative judgement in selecting its structure and distributional assumptions, regardless of whether informative prior distributions are adopted.
- Second, except in rather simple situations there may not be an agreed “objective” prior, and apparently innocuous assumptions can strongly influence conclusions in some circumstances.
The impact of choosing different a and b for beta(a,b)
- If we have little or no prior information, or we want to put very little stock in the information we have, we can choose values for \(a\) and \(b\) that reduce the distribution to a uniform distribution.
For example, if we let \(a=1\) and \(b=1\), we get \(beta(1,1)=1\) which is proportional to a uniform distribution on the allowable interval for response rate \(p\) (\([0,1]\)).
That is, the prior distribution is flat, not producing greater a priori weight for any value of \(p\) over another. Thus, the prior distribution will have little effect on the posterior distribution. For this reason, this type of prior is called “non-informative.”
- At the opposite extreme, if we have considerable prior information and we want it to weigh heavily relative to the current data, we can use large values of \(a\) and \(b\).
A little algebraic manipulation of the formula for the variance reveals that, as \(a\) and \(b\) increase, the variance decreases, which makes sense, because adding additional prior information ought to reduce our uncertainty about the parameter.
Thus, adding more prior successes and failures (increasing both parameters) reduces prior uncertainty about the parameter of interest (\(p\)).
- Finally, if we have considerable prior information but we do not wish for it to weigh heavily in the posterior distribution, we can choose moderate values of the parameters that yield a mean that is consistent with the previous research but that also produce a variance around that mean that is broad.
Example for the relationship among Prior/Likelihood/Posterior
Minimally informative prior \(Beta(0.6, 0.4)\)/\(Beta(1, 1)\)
We can see that the prior distribution \(Beta(0.6, 0.4)\)/\(Beta(1, 1)\) has little effect on the posterior distribution.1
2
3
4
5library(LearnBayes)
prior=c(0.6,0.4) # proportion has a beta(0.6, 0.4) prior
data=c(4,6) # observe 4 successes and 6 failures based on our simulated dataset
triplot(prior,data)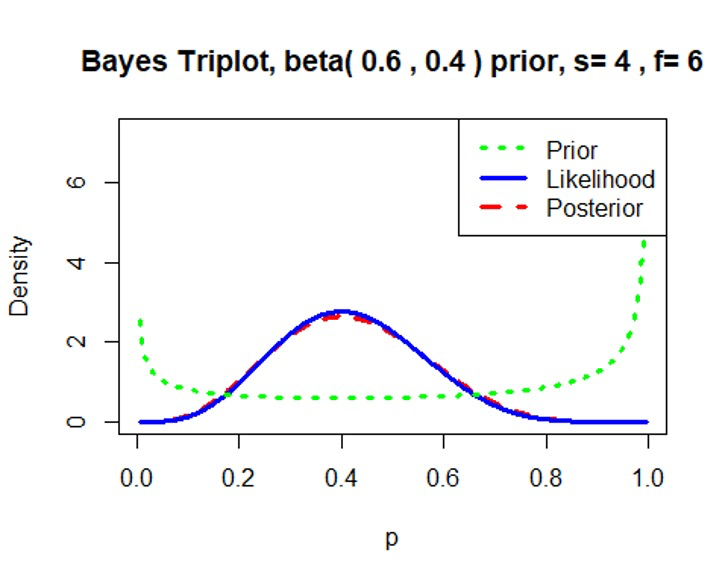
1
2
3prior=c(1,1) # proportion has a beta(1, 1) prior
data=c(4,6) # observe 4 successes and 6 failures based on our simulated dataset
triplot(prior,data)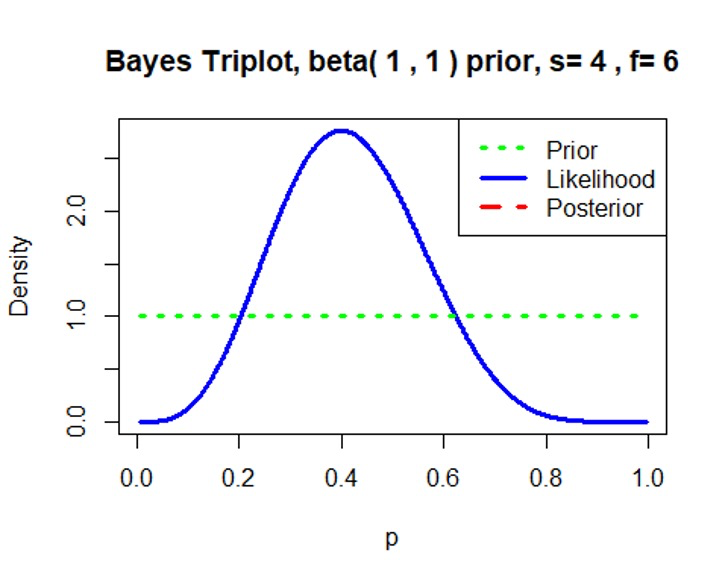
Informative prior \(Beta(6, 4)\)
We can see that the prior distribution \(Beta(6, 4)\) has considerable prior information and weigh heavily in the posterior distribution.1
2
3prior=c(6,4) # proportion has a beta(6, 4) prior
data=c(4,6) # observe 4 successes and 6 failures based on our simulated dataset
triplot(prior,data)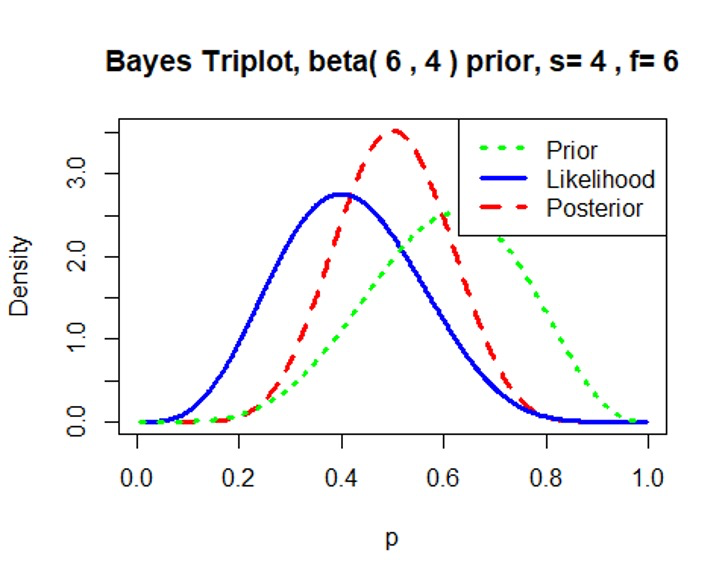
Appendix A
Type I error and power calculation using analytical methods
Method 1
Dong, G., et al (2012)
For the first stage, \(n_1\) patients are enrolled in the study. If the number of responses \(r_1\) at 1st stage is greater than or equal to the upper boundary \(u_1\) (\(r_1 \ge u_1\)), then reject the null hypothesis \(H_0: p \le p_0\) (\(H_0: p \ge p_1\)) and stop the trial for efficacy. The probability of rejecting the null hypothesis is
\[ R_1(p)=P(R_1\ge u_1 \mid p)=1-P(R_1 < u_1 \mid p)=1-F_{Bin}(p,u_1-1,n_1) \] where \(F_{Bin}\) denotes cumulative binomial distribution function.
If \(r_1\le l_1\) (the lower boundary), then accept the null hypothesis and stop the trial because of futility. The probability of accepting the null hypothesis is
\[ A_1(p)=P(R_1\le l_1 \mid p)=F_{Bin}(p,l_1,n_1) \] Otherwise, if \(r_1\) is between \(l_1\) and \(u_1\) (\(l_1 < r_1 < u_1\)), then continue the trial and enroll \(n_2\) patients into 2nd stage.
Suppose there are \(r_2\) responses observed in the \(n_2\) patients in 2nd stage. If the cumulative number of the responses \(R=R_1+R_2\) is greater than or equal to \(C\) (\(R\ge C\)), then reject the null hypothesis and claim that further investigation of the study therapy is warranted. The probability of rejecting the null hypothesis at the 2nd stage is
\[ \begin{align*} R_2(p) &= P(l_1 < R_1 < u_1, R \ge C \mid p)\\ &= \sum_{r_1=l_1+1}^{u_1-1}f_{Bin}(p,r_1,n_1)[1-F_{Bin}(p,C-r_1-1,n_2)] \end{align*} \] where \(f_{Bin}\) is the probability density function of binomial distribution. Otherwise, the test treatment is not promising and no further investigation is warranted.
For the frequentist setting, it is important to control Type I error rate and maintain study power:
Type I error rate
\[ \alpha = R_1(p_0)+R_2(p_0) \]
Power
\[ Power=1-\beta= R_1(p_1)+R_2(p_1) \]
Method 2
Chen DT, et al (2019)
First of all, \(k\) is the minimum of responders to claim efficacy with a total of \(n\) patients, and \(k_{Cum,i}\) is the number of responders for the stopping boundary at \(l\)th stage to indicate unfavorable likelihood for success. Here we have
\[ k_{Cum,l}=\sum_{i=1}^{l}k_i, \] where \(k_i\) is the additional number of responders needed in stage \(i\).
For \(k_{Cum,l}\), which is the stopping boundary at \(l\)th stage can be easily calculated by the beta-binomial distribution
\[ k_{Cum,l}=\textrm{arg min}_W\textrm{ }s \] To find the minimum \(W\) with searching \(s\) to meet \(W>0\)
\[ W=\gamma-Prob(X\ge k-s \mid n^*,a+s,b+(n_{Cum,l}-s)) \]
where \(\gamma\) is the cut-off of the predictive probability, \(n^*\) is the remaining patients given \(s\) responders in the current stage of interim analysis.
Define PET: It is a probability to stop the trial before going to the final stage. For a two-stage design, it is the probability of trial termination at the 1st stage:
\[ PET(p)=P(X \le k_1 \mid p,n_1)=\sum_{i=0}^{k_1}C_{n_1}^{i}p^i(1-p^i)^{n_1-i} \] Type I error: It is a probability of accepting treatment efficacy when the true response rate is \(p_0\). The probability is \(1-\) the sum of \(PET(p_0)\) and the probability of failure to reach the efficacy at the final stage. That is, for a \(m-\)stage design,
\[ 1-\left[ PET(p_0)+\sum_{i=k_{m-1}+1}^{min(k-1,n_{m-1})} \left[ \prod_{l=1}^{m-1} P(X=t_l \mid p_0,n_l,t_l>k_l,\sum t_l=i) \right] \times P(X \le (k-1-i) \mid p_0,n_m) \right] \] For a 2-stage design, Type I error is
\[ 1-\left[ P(X \le k_1 \mid p_0,n_1)+\sum_{i=k_{1}+1}^{min(k-1,n_1)} \left[ P(X=i \mid p_0,n_1) \right] \times P(X \le (k-1-i) \mid p_0,n_2) \right] \]
Power: It is a probability of claiming efficacy when the true response rate is \(p_1\). That is,
\[ 1-\left[ PET(p_1)+\sum_{i=k_{m-1}+1}^{min(k-1,n_{m-1})} \left[ \prod_{l=1}^{m-1} P(X=t_l \mid p_1,n_l,t_l>k_l,\sum t_l=i) \right] \times P(X \le (k-1-i) \mid p_1,n_m) \right] \]
Appendix B
1 | # run |
Table 5: The result of searching the combination of r, theta_t and theta_l with fixed total sample size
| N | r | theta_t | theta_l | Type_I | Type_II |
|---|---|---|---|---|---|
| 36 | 10 | 0.7 | 0.001 | 0.0382 | 0.166 |
| 36 | 10 | 0.701 | 0.001 | 0.0475 | 0.165 |
| 36 | 10 | 0.702 | 0.001 | 0.0415 | 0.169 |
| 36 | 10 | 0.703 | 0.001 | 0.0475 | 0.164 |
| 36 | 10 | 0.704 | 0.001 | 0.0418 | 0.158 |
| 36 | 10 | 0.705 | 0.001 | 0.042 | 0.168 |
| 36 | 10 | 0.706 | 0.001 | 0.0345 | 0.161 |
| 36 | 10 | 0.707 | 0.001 | 0.0408 | 0.159 |
| 36 | 10 | 0.708 | 0.001 | 0.0413 | 0.171 |
| 36 | 10 | 0.709 | 0.001 | 0.0365 | 0.163 |
| 36 | 10 | 0.71 | 0.001 | 0.0408 | 0.155 |
| 36 | 10 | 0.711 | 0.001 | 0.0385 | 0.167 |
| 36 | 10 | 0.712 | 0.001 | 0.0455 | 0.164 |
| 36 | 10 | 0.713 | 0.001 | 0.043 | 0.163 |
| 36 | 10 | 0.714 | 0.001 | 0.0372 | 0.163 |
| 36 | 10 | 0.715 | 0.001 | 0.0423 | 0.156 |
| 36 | 10 | 0.716 | 0.001 | 0.0398 | 0.157 |
| 36 | 10 | 0.717 | 0.001 | 0.04 | 0.167 |
| 36 | 10 | 0.718 | 0.001 | 0.0413 | 0.158 |
| 36 | 10 | 0.719 | 0.001 | 0.0403 | 0.167 |
| 36 | 10 | 0.72 | 0.001 | 0.0432 | 0.166 |
| 36 | 10 | 0.721 | 0.001 | 0.0428 | 0.163 |
| 36 | 10 | 0.722 | 0.001 | 0.04 | 0.173 |
| 36 | 10 | 0.723 | 0.001 | 0.0415 | 0.159 |
| 36 | 10 | 0.724 | 0.001 | 0.0408 | 0.172 |
| 36 | 10 | 0.725 | 0.001 | 0.0408 | 0.154 |
| 36 | 10 | 0.726 | 0.001 | 0.043 | 0.168 |
| 36 | 10 | 0.727 | 0.001 | 0.043 | 0.161 |
| 36 | 10 | 0.728 | 0.001 | 0.043 | 0.168 |
| 36 | 10 | 0.729 | 0.001 | 0.048 | 0.16 |
| 36 | 10 | 0.73 | 0.001 | 0.037 | 0.16 |
| 36 | 10 | 0.731 | 0.001 | 0.0382 | 0.153 |
| 36 | 10 | 0.732 | 0.001 | 0.0445 | 0.159 |
| 36 | 10 | 0.733 | 0.001 | 0.0445 | 0.162 |
| 36 | 10 | 0.734 | 0.001 | 0.0472 | 0.152 |
| 36 | 10 | 0.735 | 0.001 | 0.0478 | 0.16 |
| 36 | 10 | 0.736 | 0.001 | 0.0398 | 0.167 |
| 36 | 10 | 0.737 | 0.001 | 0.045 | 0.162 |
| 36 | 10 | 0.738 | 0.001 | 0.0415 | 0.171 |
| 36 | 10 | 0.739 | 0.001 | 0.0398 | 0.173 |
| 36 | 10 | 0.74 | 0.001 | 0.0452 | 0.158 |
| 36 | 10 | 0.741 | 0.001 | 0.0425 | 0.17 |
| 36 | 10 | 0.742 | 0.001 | 0.0425 | 0.168 |
| 36 | 10 | 0.743 | 0.001 | 0.0445 | 0.164 |
| 36 | 10 | 0.744 | 0.001 | 0.0365 | 0.168 |
| 36 | 10 | 0.745 | 0.001 | 0.041 | 0.161 |
| 36 | 10 | 0.746 | 0.001 | 0.0423 | 0.17 |
| 36 | 10 | 0.747 | 0.001 | 0.046 | 0.152 |
| 36 | 10 | 0.748 | 0.001 | 0.0355 | 0.157 |
| 36 | 10 | 0.749 | 0.001 | 0.0457 | 0.168 |
| 36 | 10 | 0.75 | 0.001 | 0.0493 | 0.162 |
| 36 | 10 | 0.751 | 0.001 | 0.0437 | 0.161 |
| 36 | 10 | 0.752 | 0.001 | 0.0415 | 0.16 |
| 36 | 10 | 0.753 | 0.001 | 0.0395 | 0.169 |
| 36 | 10 | 0.754 | 0.001 | 0.0483 | 0.159 |
| 36 | 10 | 0.755 | 0.001 | 0.0437 | 0.166 |
| 36 | 10 | 0.756 | 0.001 | 0.0425 | 0.167 |
| 36 | 10 | 0.757 | 0.001 | 0.0432 | 0.165 |
| 36 | 10 | 0.758 | 0.001 | 0.042 | 0.161 |
| 36 | 10 | 0.759 | 0.001 | 0.04 | 0.166 |
| 36 | 10 | 0.76 | 0.001 | 0.0403 | 0.163 |
| 36 | 10 | 0.761 | 0.001 | 0.039 | 0.164 |
| 36 | 10 | 0.762 | 0.001 | 0.043 | 0.156 |
| 36 | 10 | 0.763 | 0.001 | 0.043 | 0.155 |
| 36 | 10 | 0.764 | 0.001 | 0.045 | 0.16 |
| 36 | 10 | 0.765 | 0.001 | 0.0405 | 0.165 |
| 36 | 10 | 0.766 | 0.001 | 0.0403 | 0.162 |
| 36 | 10 | 0.767 | 0.001 | 0.0408 | 0.147 |
| 36 | 10 | 0.768 | 0.001 | 0.0442 | 0.163 |
| 36 | 10 | 0.769 | 0.001 | 0.0398 | 0.164 |
| 36 | 10 | 0.77 | 0.001 | 0.046 | 0.157 |
| 36 | 10 | 0.771 | 0.001 | 0.04 | 0.165 |
| 36 | 10 | 0.772 | 0.001 | 0.0478 | 0.163 |
| 36 | 10 | 0.773 | 0.001 | 0.0403 | 0.168 |
| 36 | 10 | 0.774 | 0.001 | 0.0442 | 0.172 |
| 36 | 10 | 0.775 | 0.001 | 0.045 | 0.167 |
| 36 | 10 | 0.776 | 0.001 | 0.0372 | 0.172 |
| 36 | 10 | 0.777 | 0.001 | 0.046 | 0.157 |
| 36 | 10 | 0.778 | 0.001 | 0.04 | 0.17 |
| 36 | 10 | 0.779 | 0.001 | 0.0403 | 0.17 |
| 36 | 10 | 0.78 | 0.001 | 0.0425 | 0.16 |
| 36 | 10 | 0.781 | 0.001 | 0.0415 | 0.161 |
| 36 | 10 | 0.782 | 0.001 | 0.0472 | 0.166 |
| 36 | 10 | 0.783 | 0.001 | 0.039 | 0.161 |
| 36 | 10 | 0.784 | 0.001 | 0.04 | 0.17 |
| 36 | 10 | 0.785 | 0.001 | 0.042 | 0.167 |
| 36 | 10 | 0.786 | 0.001 | 0.0465 | 0.158 |
| 36 | 10 | 0.787 | 0.001 | 0.044 | 0.17 |
| 36 | 10 | 0.788 | 0.001 | 0.0375 | 0.155 |
| 36 | 10 | 0.789 | 0.001 | 0.0435 | 0.162 |
| 36 | 10 | 0.79 | 0.001 | 0.0398 | 0.163 |
| 36 | 10 | 0.791 | 0.001 | 0.0418 | 0.158 |
| 36 | 10 | 0.792 | 0.001 | 0.0367 | 0.159 |
| 36 | 10 | 0.793 | 0.001 | 0.0385 | 0.158 |
| 36 | 10 | 0.794 | 0.001 | 0.0478 | 0.173 |
| 36 | 10 | 0.795 | 0.001 | 0.043 | 0.165 |
| 36 | 10 | 0.796 | 0.001 | 0.0357 | 0.158 |
| 36 | 10 | 0.797 | 0.001 | 0.0428 | 0.168 |
| 36 | 10 | 0.798 | 0.001 | 0.044 | 0.166 |
| 36 | 10 | 0.799 | 0.001 | 0.0415 | 0.157 |
| 36 | 10 | 0.8 | 0.001 | 0.0398 | 0.161 |
| 36 | 10 | 0.801 | 0.001 | 0.041 | 0.158 |
| 36 | 10 | 0.802 | 0.001 | 0.038 | 0.162 |
| 36 | 10 | 0.803 | 0.001 | 0.0465 | 0.165 |
| 36 | 10 | 0.804 | 0.001 | 0.0428 | 0.169 |
| 36 | 10 | 0.805 | 0.001 | 0.04 | 0.164 |
| 36 | 10 | 0.806 | 0.001 | 0.0403 | 0.164 |
| 36 | 10 | 0.807 | 0.001 | 0.041 | 0.158 |
| 36 | 10 | 0.808 | 0.001 | 0.0395 | 0.169 |
| 36 | 10 | 0.809 | 0.001 | 0.0493 | 0.159 |
| 36 | 10 | 0.81 | 0.001 | 0.0442 | 0.171 |
| 36 | 10 | 0.811 | 0.001 | 0.043 | 0.166 |
| 36 | 10 | 0.812 | 0.001 | 0.0385 | 0.165 |
| 36 | 10 | 0.813 | 0.001 | 0.0372 | 0.167 |
| 36 | 10 | 0.814 | 0.001 | 0.0418 | 0.152 |
| 36 | 10 | 0.815 | 0.001 | 0.0465 | 0.16 |
| 36 | 10 | 0.816 | 0.001 | 0.0405 | 0.165 |
| 36 | 10 | 0.817 | 0.001 | 0.0423 | 0.166 |
| 36 | 10 | 0.818 | 0.001 | 0.0445 | 0.166 |
| 36 | 10 | 0.819 | 0.001 | 0.0385 | 0.164 |
| 36 | 10 | 0.82 | 0.001 | 0.0447 | 0.163 |
| 36 | 10 | 0.821 | 0.001 | 0.042 | 0.165 |
| 36 | 10 | 0.822 | 0.001 | 0.0442 | 0.162 |
| 36 | 10 | 0.823 | 0.001 | 0.0405 | 0.167 |
| 36 | 10 | 0.824 | 0.001 | 0.0428 | 0.165 |
| 36 | 10 | 0.825 | 0.001 | 0.0428 | 0.174 |
| 36 | 10 | 0.826 | 0.001 | 0.0403 | 0.161 |
| 36 | 10 | 0.827 | 0.001 | 0.0387 | 0.161 |
| 36 | 10 | 0.828 | 0.001 | 0.0445 | 0.165 |
| 36 | 10 | 0.829 | 0.001 | 0.0382 | 0.164 |
| 36 | 10 | 0.83 | 0.001 | 0.0408 | 0.16 |
| 36 | 10 | 0.831 | 0.001 | 0.0442 | 0.156 |
| 36 | 10 | 0.832 | 0.001 | 0.046 | 0.166 |
| 36 | 10 | 0.833 | 0.001 | 0.0377 | 0.16 |
| 36 | 10 | 0.834 | 0.001 | 0.0398 | 0.16 |
| 36 | 10 | 0.835 | 0.001 | 0.0435 | 0.167 |
| 36 | 10 | 0.836 | 0.001 | 0.046 | 0.162 |
| 36 | 10 | 0.837 | 0.001 | 0.0445 | 0.167 |
| 36 | 10 | 0.838 | 0.001 | 0.0467 | 0.176 |
| 36 | 10 | 0.839 | 0.001 | 0.0442 | 0.146 |
| 36 | 10 | 0.84 | 0.001 | 0.04 | 0.168 |
| 36 | 10 | 0.841 | 0.001 | 0.0423 | 0.165 |
| 36 | 10 | 0.842 | 0.001 | 0.042 | 0.155 |
| 36 | 10 | 0.843 | 0.001 | 0.0428 | 0.162 |
| 36 | 10 | 0.844 | 0.001 | 0.04 | 0.17 |
| 36 | 10 | 0.845 | 0.001 | 0.0452 | 0.156 |
| 36 | 10 | 0.846 | 0.001 | 0.0452 | 0.157 |
| 36 | 10 | 0.847 | 0.001 | 0.0392 | 0.17 |
| 36 | 10 | 0.848 | 0.001 | 0.0465 | 0.178 |
| 36 | 10 | 0.849 | 0.001 | 0.0357 | 0.16 |
| 36 | 10 | 0.85 | 0.001 | 0.0387 | 0.163 |
| 36 | 10 | 0.851 | 0.001 | 0.0382 | 0.163 |
| 36 | 10 | 0.852 | 0.001 | 0.0425 | 0.16 |
| 36 | 10 | 0.853 | 0.001 | 0.0435 | 0.166 |
| 36 | 10 | 0.854 | 0.001 | 0.0442 | 0.16 |
| 36 | 10 | 0.855 | 0.001 | 0.0432 | 0.17 |
| 36 | 10 | 0.856 | 0.001 | 0.0432 | 0.169 |
| 36 | 10 | 0.857 | 0.001 | 0.0437 | 0.164 |
| 36 | 10 | 0.858 | 0.001 | 0.0395 | 0.162 |
| 36 | 10 | 0.859 | 0.001 | 0.0428 | 0.154 |
| 36 | 10 | 0.86 | 0.001 | 0.041 | 0.168 |
| 36 | 10 | 0.861 | 0.001 | 0.0408 | 0.154 |
| 36 | 10 | 0.862 | 0.001 | 0.0408 | 0.169 |
| 36 | 10 | 0.863 | 0.001 | 0.0413 | 0.163 |
| 36 | 10 | 0.864 | 0.001 | 0.0435 | 0.168 |
| 36 | 10 | 0.865 | 0.001 | 0.0467 | 0.168 |
| 36 | 10 | 0.866 | 0.001 | 0.0403 | 0.169 |
| 36 | 10 | 0.867 | 0.001 | 0.0385 | 0.169 |
| 36 | 10 | 0.868 | 0.001 | 0.0432 | 0.167 |
| 36 | 10 | 0.869 | 0.001 | 0.041 | 0.161 |
| 36 | 10 | 0.87 | 0.001 | 0.0425 | 0.16 |
| 36 | 10 | 0.871 | 0.001 | 0.0405 | 0.166 |
| 36 | 10 | 0.872 | 0.001 | 0.0395 | 0.155 |
| 36 | 10 | 0.873 | 0.001 | 0.0423 | 0.175 |
| 36 | 10 | 0.874 | 0.001 | 0.0442 | 0.169 |
| 36 | 10 | 0.875 | 0.001 | 0.0485 | 0.168 |
| 36 | 10 | 0.876 | 0.001 | 0.0357 | 0.172 |
| 36 | 10 | 0.877 | 0.001 | 0.0398 | 0.154 |
| 36 | 10 | 0.878 | 0.001 | 0.0432 | 0.171 |
| 36 | 10 | 0.879 | 0.001 | 0.0405 | 0.166 |
| 36 | 10 | 0.88 | 0.001 | 0.0425 | 0.168 |
| 36 | 10 | 0.881 | 0.001 | 0.0457 | 0.165 |
| 36 | 10 | 0.882 | 0.001 | 0.0432 | 0.161 |
| 36 | 10 | 0.883 | 0.001 | 0.0372 | 0.153 |
| 36 | 10 | 0.884 | 0.001 | 0.0452 | 0.158 |
| 36 | 10 | 0.885 | 0.001 | 0.043 | 0.168 |
| 36 | 10 | 0.886 | 0.001 | 0.0425 | 0.162 |
| 36 | 10 | 0.887 | 0.001 | 0.0333 | 0.17 |
| 36 | 10 | 0.888 | 0.001 | 0.04 | 0.175 |
| 36 | 10 | 0.889 | 0.001 | 0.0423 | 0.166 |
| 36 | 10 | 0.89 | 0.001 | 0.042 | 0.165 |
| 36 | 10 | 0.891 | 0.001 | 0.044 | 0.157 |
| 36 | 10 | 0.892 | 0.001 | 0.0437 | 0.168 |
| 36 | 10 | 0.893 | 0.001 | 0.0415 | 0.167 |
| 36 | 10 | 0.894 | 0.001 | 0.0387 | 0.153 |
| 36 | 10 | 0.895 | 0.001 | 0.046 | 0.165 |
| 36 | 10 | 0.896 | 0.001 | 0.0457 | 0.157 |
| 36 | 10 | 0.897 | 0.001 | 0.0425 | 0.156 |
| 36 | 10 | 0.898 | 0.001 | 0.0403 | 0.17 |
| 36 | 10 | 0.899 | 0.001 | 0.0423 | 0.161 |
| 36 | 10 | 0.9 | 0.001 | 0.0418 | 0.164 |
| 36 | 10 | 0.901 | 0.001 | 0.0415 | 0.171 |
| 36 | 10 | 0.902 | 0.001 | 0.0372 | 0.165 |
| 36 | 10 | 0.903 | 0.001 | 0.0472 | 0.154 |
| 36 | 10 | 0.904 | 0.001 | 0.0432 | 0.162 |
| 36 | 10 | 0.905 | 0.001 | 0.045 | 0.166 |
| 36 | 10 | 0.906 | 0.001 | 0.0395 | 0.169 |
| 36 | 10 | 0.907 | 0.001 | 0.0435 | 0.164 |
| 36 | 10 | 0.908 | 0.001 | 0.0415 | 0.162 |
| 36 | 10 | 0.909 | 0.001 | 0.041 | 0.167 |
| 36 | 10 | 0.91 | 0.001 | 0.0423 | 0.161 |
| 36 | 10 | 0.911 | 0.001 | 0.0442 | 0.17 |
| 36 | 10 | 0.912 | 0.001 | 0.044 | 0.167 |
| 36 | 10 | 0.913 | 0.001 | 0.0408 | 0.162 |
| 36 | 10 | 0.914 | 0.001 | 0.0395 | 0.167 |
| 36 | 10 | 0.915 | 0.001 | 0.0415 | 0.167 |
| 36 | 10 | 0.916 | 0.001 | 0.05 | 0.174 |
| 36 | 10 | 0.917 | 0.001 | 0.0425 | 0.157 |
| 36 | 10 | 0.918 | 0.001 | 0.0375 | 0.165 |
| 36 | 10 | 0.919 | 0.001 | 0.047 | 0.165 |
| 36 | 10 | 0.92 | 0.001 | 0.0408 | 0.17 |
| 36 | 10 | 0.921 | 0.001 | 0.0423 | 0.161 |
| 36 | 10 | 0.922 | 0.001 | 0.0442 | 0.151 |
| 36 | 10 | 0.923 | 0.001 | 0.0415 | 0.169 |
| 36 | 10 | 0.924 | 0.001 | 0.0385 | 0.174 |
| 36 | 10 | 0.925 | 0.001 | 0.0413 | 0.171 |
| 36 | 10 | 0.926 | 0.001 | 0.0377 | 0.161 |
| 36 | 10 | 0.927 | 0.001 | 0.0387 | 0.16 |
| 36 | 10 | 0.928 | 0.001 | 0.043 | 0.165 |
| 36 | 10 | 0.929 | 0.001 | 0.0423 | 0.158 |
| 36 | 10 | 0.93 | 0.001 | 0.0465 | 0.156 |
| 36 | 10 | 0.931 | 0.001 | 0.0437 | 0.157 |
| 36 | 10 | 0.932 | 0.001 | 0.0377 | 0.17 |
| 36 | 10 | 0.933 | 0.001 | 0.0452 | 0.164 |
| 36 | 10 | 0.934 | 0.001 | 0.048 | 0.154 |
| 36 | 10 | 0.935 | 0.001 | 0.0472 | 0.171 |
| 36 | 10 | 0.936 | 0.001 | 0.0485 | 0.165 |
| 36 | 10 | 0.937 | 0.001 | 0.0415 | 0.159 |
| 36 | 10 | 0.938 | 0.001 | 0.0408 | 0.18 |
| 36 | 10 | 0.939 | 0.001 | 0.042 | 0.166 |
| 36 | 10 | 0.94 | 0.001 | 0.0377 | 0.16 |
| 36 | 10 | 0.941 | 0.001 | 0.0445 | 0.165 |
| 36 | 10 | 0.942 | 0.001 | 0.0437 | 0.163 |
| 36 | 10 | 0.943 | 0.001 | 0.047 | 0.174 |
| 36 | 10 | 0.944 | 0.001 | 0.04 | 0.17 |
| 36 | 10 | 0.945 | 0.001 | 0.0437 | 0.163 |
| 36 | 10 | 0.946 | 0.001 | 0.043 | 0.171 |
| 36 | 10 | 0.947 | 0.001 | 0.04 | 0.17 |
| 36 | 10 | 0.948 | 0.001 | 0.0445 | 0.164 |
| 36 | 10 | 0.949 | 0.001 | 0.0445 | 0.171 |
| 36 | 10 | 0.95 | 0.001 | 0.0418 | 0.151 |
Reference
Chen, D. T., Schell, M. J., Fulp, W. J., Pettersson, F., Kim, S., Gray, J. E., & Haura, E. B. (2019). Application of Bayesian predictive probability for interim futility analysis in single-arm phase II trial. Translational cancer research, 8(Suppl 4), S404–S420. https://doi.org/10.21037/tcr.2019.05.17
Lee, J. J., & Liu, D. D. (2008). A predictive probability design for phase II cancer clinical trials. Clinical trials (London, England), 5(2), 93–106. https://doi.org/10.1177/1740774508089279
Dong, G., Shih, W.J., Moore, D., Quan, H. and Marcella, S. (2012), A Bayesian–frequentist two-stage single-arm phase II clinical trial design. Statist. Med., 31: 2055-2067. https://doi.org/10.1002/sim.5330