Sequential Enrichment Designs for Early Phase Clinical Trials (Reproducing Results)
This post reproduces the results from the presentation Sequential Enrichment Designs for Early Phase Clinical Trials.
Background
Study objective
- PoC study of Drug A to evaluate its anti-tumor activity in gastric cancer
Endpoint
- Objective response rate (ORR) Study population
- All patients irrespective of status for biomarker of interest Y
Study design
- Single-arm with biomarker of interest Y
Dual Criteria Design
- Formal inclusion of statistical significance and clinical relevance in design:
- Decide GO
- Strong evidence: effect ≥ no effect or null value (NV)
- Estimated effect ≥ decision value (DV)
- DV : minimum effect with clinical relevance; not classical alternative hypothesis
- Need discussion with nonstatisticians
- Sample size requires consideration of DV
- Adequate sample size is required to ensure statistical significance when clinical relevance observed
- Need simulation to calculate design operating characteristics (e.g., type-I error, power)
Subpopulation Selection in Early Phase
Demand for a new design
- A competitor Drug B failed for all-comers but show promising efficacy in patients with Y+ in post-hoc subgroup analysis
Goal
- Assess activity of Drug A for all patients irrespective of biomarker status
- If it is not active for all patients, assess activity of Drug A for Y+ patients
Single-stage Design with Population Selection
Brief Description
Study populations All-comers (F) = Y+ patients + Y- patients
Bayesian triplet criterion for all-comers
- Pr(ORR (F) ≥ 16% | data) ≥ 0.975
- Posterior median (F) ≥ 24%
- Pr(ORR (Y-) ≥ 16% | data) ≥ 0.75 (activity assurance in Y- patients)
The third criteria ensures that the effect of Drug A in F is not solely driven by Y+
- Bayesian dual criteria for Y+ patients
- Pr(ORR (Y+) ≥ 16% | data) ≥ 0.95
- Posterior median (Y+) ≥ 24%
- Minimum sample size (SSmin) All-comers: 87 (with number of responders ≥21) Y+ patients: 58 (with number of responders ≥14)
Sample size bigger than SSmin ensures statistical significance when clinical relevance is observed
Figure 1: Flow Chart for Single-stage Enrichment Design
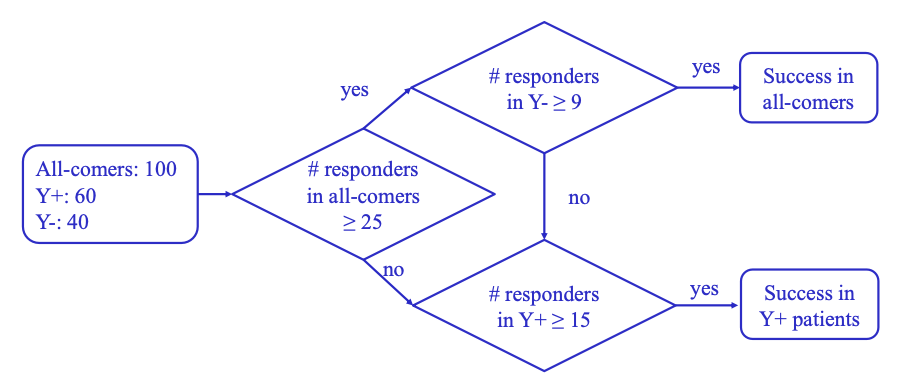
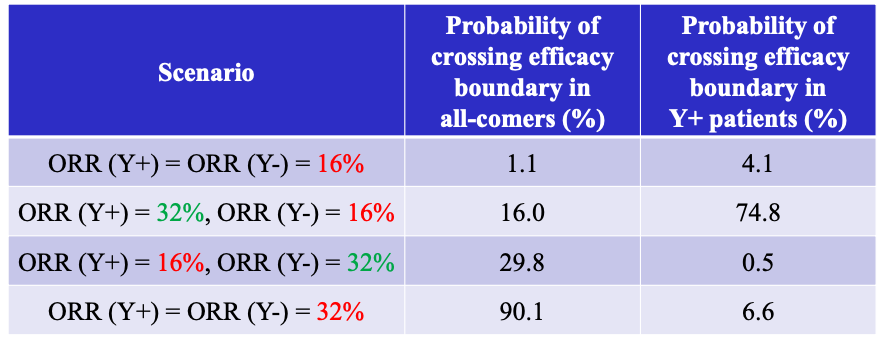
Figure 2: OC for One-stage Enrichment Design
Main Body of R Code
1 | ####################################################################### |
Utility Function
1 |
|
OC
1 | OC for One stage Enrichment Design |
Two-stage Design with Adaptive Population Enrichment
Brief Description
- Sequential enrichment
- Use probability of success (POS) at interim to allow early stopping for futility.
- Use POS for interim decision making
- POS(F): PP(posterior median (F) ≥ 24% at final analysis | interim data); PP=predictive probability
- POS(Y+): PP(posterior median (Y+) ≥ 24% at final analysis | interim data)
- POS(Y-): PP (Pr(ORR (Y-) ≥ 16% | data) ≥ 0.75 at final analysis | interim data)
- Interim decision rules
- Continue with F: POS(F) ≥ 10% and POS(Y-) ≥ 10%
- Continue with Y+: POS(F) ≥ 10% but POS(Y-) < 10% and POS(Y+) ≥ 10% OR
- POS(F) < 10% but POS(Y+) ≥ 10%
Otherwise stop for futility.
Figure 3: Flow Chart for Sequential Enrichment Design

Figure 4: Interim OC for Sequential Enrichment Design
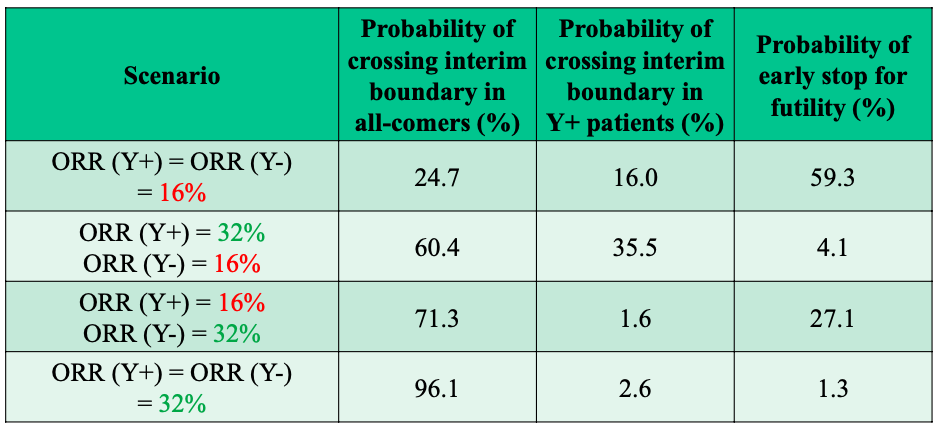
Figure 5: Final OC for Sequential Enrichment Design
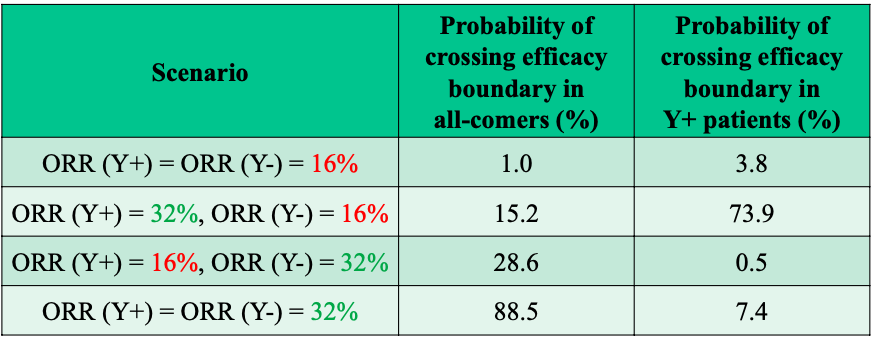
Main Body of R Code
1 | ####################################################################### |
Utility Function
function_cpp.cpp1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
using namespace Rcpp;
// [[Rcpp::export]]
NumericVector responsegate(int maxresponse,int samplesizestart,int maxsamplesize,double a,double b,double nv,double positivestatsig,double statsig,double postmed){
// Creating object
int row,totalrow,f1,f2,f3;
double med,sig;
totalrow = (maxsamplesize-samplesizestart+1)*(maxresponse);
NumericMatrix df(totalrow,8);
row = 0;
// using loop to construct response matrix
for(int r = 1; r <= maxresponse; ++r) {
for(int n = samplesizestart; n <= maxsamplesize; ++n) {
// generate beta random numbers
NumericVector rand = Rcpp::rbeta( 100000, a+r, b+n-r);
// compare to nv
LogicalVector logicnv = rand >= nv;
sig= mean(logicnv);
med = median(rand);
// output
df(row,0) = r;
df(row,1) = n;
df(row,2)=sig;
df(row,3)=med;
// decision flag
f1=0;
f2=0;
f3=0;
if (sig<positivestatsig && med>=postmed){
df(row,4)=1;
f1=1;
};
if (sig>=positivestatsig && med>=postmed && sig<statsig){
df(row,5)=1;
f2=1;
};
if (sig>=statsig && med>=postmed){
df(row,6)=1;
f3=1;
};
// 2-full,3-positive only,4-n/a
if (f3==1){
df(row,7) = 2;
} else if(f2==1){
df(row,7) = 3;
} else if (f1==1){
df(row,7) = 4;
}
row++;
}
}
return df;
}
predprobMedian.cpp1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
using namespace Rcpp;
// [[Rcpp::export]]
double predprobMedian(int x, int n, int nmax, double alpha, double beta, double theta_t) {
double prob = 0.0;
double eps = std::numeric_limits<double>::epsilon();
double med;
for (int resp = 0; resp < nmax - n + 1; resp++) {
// --------------------------------------------------------
// --- use median instead of posterior in pfizer's settings
// --------------------------------------------------------
// generate beta random numbers
NumericVector rand = Rcpp::rbeta( 100000, alpha + x + resp, beta + nmax - x - resp);
med = median(rand);
if (med > theta_t || std::abs(med - theta_t) < eps) {
prob += exp(
R::lchoose(nmax - n, resp) +
R::lbeta(alpha + x + resp, beta + nmax - x - resp) -
R::lbeta(alpha + x, beta + n - x)
);
}
}
return prob;
}
predprobPosterior.cpp1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
using namespace Rcpp;
// [[Rcpp::export]]
double predprobPosterior(int x, int n, int nmax, double alpha, double beta, double p0, double theta_t){
double prob = 0.0;
double eps = std::numeric_limits<double>::epsilon();
double pxy;
for (int resp = 0; resp < nmax - n + 1; resp++) {
pxy = (1.0 - R::pbeta(p0, alpha + resp + x, beta + nmax - resp - x, 1, 0));
if (pxy > theta_t || std::abs(pxy - theta_t) < eps) {
prob += exp(
R::lchoose(nmax - n, resp) +
R::lbeta(alpha + resp + x, beta + nmax - resp - x) -
R::lbeta(alpha + x, beta + n - x)
);
}
}
return prob;
}
OC
1 |
|
Appendix - Comparison of R & RCPP
1 | library(Rcpp) |