Background

Issue of analysis methods

Recently, we received FDA response for the model selection. We tried to use a logistic regression model with baseline scores as the covariate to estimate the odds ratio (OR). The objective is to show the superiority on a binary endpoint.

FDA wrote:

7. We recommend that the primary and secondary efficacy analyses focus on estimating and testing the difference in the proportions of responders between the treatment groups. Your proposed efficacy analysis appears to estimate the conditional odds ratio using a logistic regression model with baseline grade as a covariate. This analysis assumes that the odds ratio is the same for different baseline grade. In general. the true conditional odds ratios may differ across the covariate levels. Even if the odds ratio across the covariate levels are the same. this common odds ratio may differ from the population-wide odds ratio. Therefore, you should clearly describe in the SAP why the set of conditional odds ratios is more relevant compared to the population-wide odds ratio or the population difference in the rates of responders.

FDA guidance on adjusting for covariates in RCTs

In the FDA guidance part C. Nonlinear models, it says

1. Covariate adjustment with nonlinear models is often used in the analysis of clinical trial data when the primary outcome of interest is not measured on a continuous scale or is right censored (e.g., binary outcome, ordinal outcome, count outcome, or time-to-event outcome). Adjustment using nonlinear models is a potentially acceptable method for analyzing these data from a clinical trial. However, there are additional issues described below that should be considered before using nonlinear models.

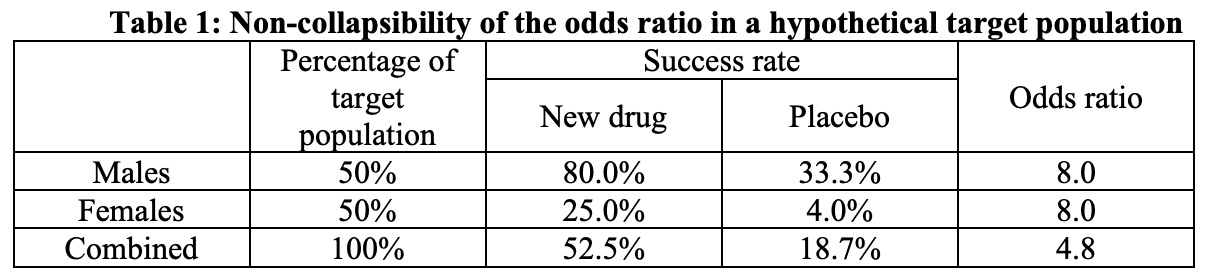
2. In general, treatment effects may differ from subgroup to subgroup. However, with some parameters such as odds ratios, even when all subgroup treatment effects are identical this subgroup-specific conditional treatment effect can differ from the unconditional treatment effect (i.e., the effect at the population level from moving the target population from untreated to treated) (Gail et al. 1984). This is termed non-collapsibility (Agresti 2002), which is distinct from confounding and can occur despite randomization and large sample sizes. An example of non-collapsibility of the odds ratio for a hypothetical clinical trial is illustrated in Table below. The unconditional odds ratio in the hypothetical target population is 4.8, which is lower than the conditional odds ratio of 8.0 in each of the male and female subgroups. In trials with time-to-event outcomes, the hazard ratio is also generally non-collapsible. Unlike the odds ratio or hazard ratio, the risk difference and relative risk are collapsible.

3. Fitting a nonlinear regression of the outcome on treatment and baseline covariates similarly attempts to estimate a conditional treatment effect.拟合这种非线性回归模型，同样试图估计的是conditional treatment effect

4. In nonlinear regression models (without treatment by covariate interactions) the treatment effect is assumed to be approximately constant across subgroups defined by baseline covariates in the model and can provide more personalized information than the unconditional treatment effect.【评论：这里非常绕。假如logistic模型里没有交互项 Treatment*Baseline，那么这里假定的是，在所有Baseline的所有水平上，疗效都是恒定的】

注：代码验证FDA指导文件Table1的结果放在附录1.

Conditional OR and Unconditional OR

Marginal Odds Ratios Marginal odds ratios are odds ratios between two variables in the marginal table and can be used to test for marginal independence between two variables while ignoring the third.

Conditional Odds Ratios Conditional odds ratios are odds ratios between two variables for fixed levels of the third variable and allow us to test for conditional independence of two variables, given the third.

Reference Link

Conditional vs unconditional effects in Linear Models

Conditional vs unconditional effects

In the guidance, it says

Covariate adjustment through a linear model (without treatment by covariate interactions) also estimates a conditional treatment effect, which is a treatment effect assumed to be approximately constant across subgroups defined by baseline covariates in the model. 通过线性模型的协变量调整（没有治疗与协变量的交互作用）,也估计了条件性治疗效果，即假定在模型中由基线协变量定义的各亚组中治疗效果大致不变。

This is saying that for linear models which don't include treatment by covariate interactions, the treatment effect estimate has both an interpretation as

1. a marginal treatment effect (how does the population mean outcome change if you switch from treatment A to B) and

2. as a conditional effect (how does the mean outcome change in subpopulations defined by levels of the covariates adjusted for).

Of course for the latter interpretation to be correct, as the quoted text says, it must be the case that in truth these conditional/subpopulation effects are identical across these subpopulations. In reality there is no reason why this will necessarily be true, certainly not exactly.为了使后一种解释正确，正如引用的文字所说，必须在现实中，这些条件/亚组效应在这些亚组中是相同的。在现实中，这很难达到。

Including interactions

The guidance notes that

The linear model may include treatment by covariate interaction terms. However, when using this approach, the primary analysis should still be based on an estimate from the model of the average treatment effect.

Conditional vs unconditional effects in Non-linear Models

Non-Collapsibility

Non-collapsibility means that the conditional ratio is different from the marginal (unadjusted) ratio even in the complete absence of confounding.

Detailed introduction could be found at stats.stackexchange.

An Example

第一步：构造模拟数据 4000 patient randomized clinical trial with one important covariate: patient sex.

The code for simulation

1
2
3
4

d <- expand.grid(y=0:1, tx=c('A','B'),sex=c('male', 'female'))
# Order treatment levels to get OR > 1
d$tx <- factor(d$tx, c('B','A'))
d$freq <- c(500, 500, 900, 100, 100, 900, 500, 500)

这个预后变量在治疗 A 和 B 上具有完美的平衡，并且在任一治疗组中： 女性：男性效应的OR为 9； 对于任何一种性别，A:B 的OR也是 9。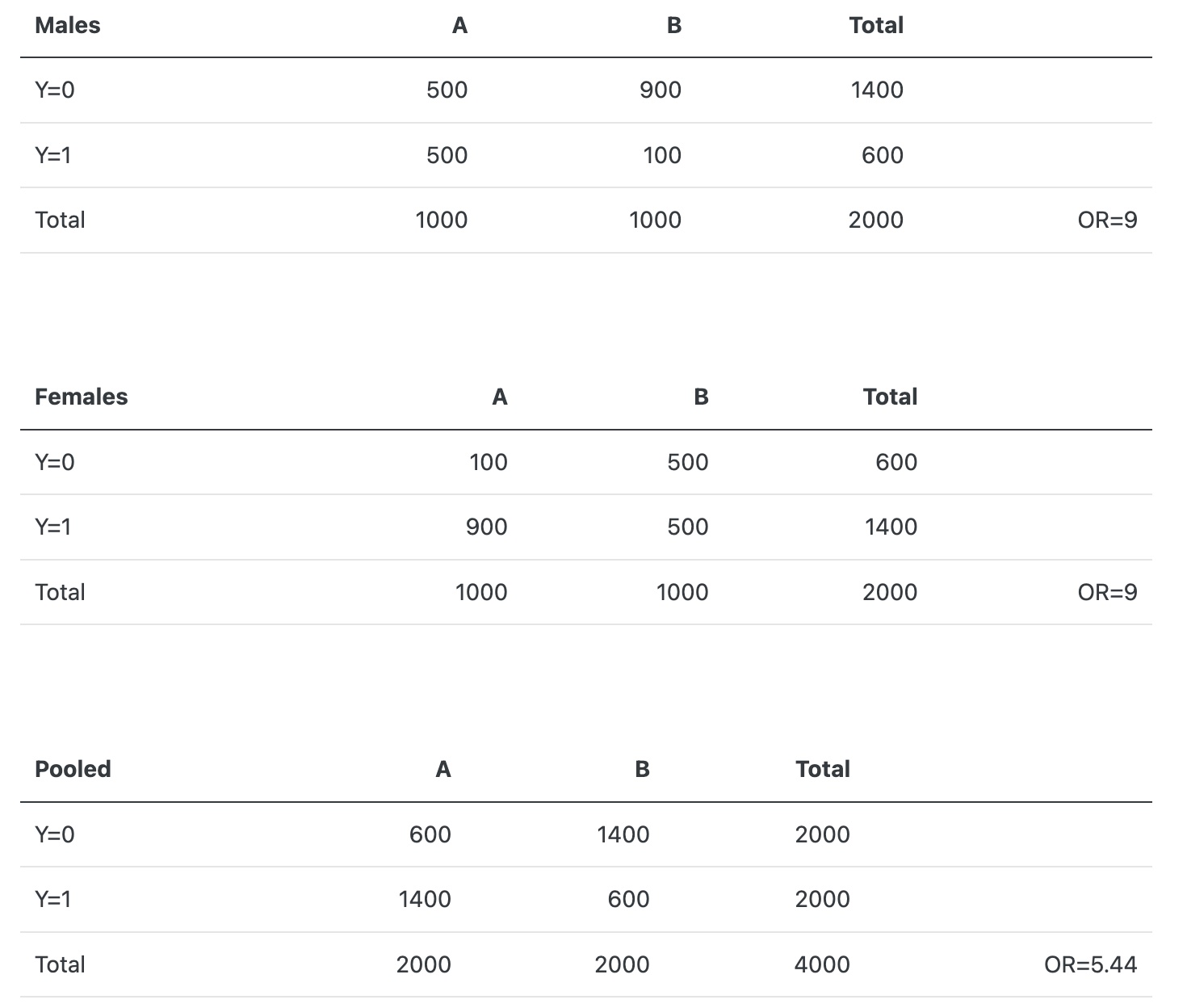

从上表，我们看到，不以患者性别为条件的 A:B 比值比为 5.44. 请注意，这不是 9 和 9 的加权平均值. 未经调整的 OR 既不适用于男性也不适用于女性.

一个微妙的问题是: pooled marginal estimates（OR = 5.44 以上）难以解释, 并且不能推广到具有不同于 RCT 样本组成的协变量分布（此处为性别）的临床人群。

我们接下来拟合一个带有sex变量的logistic模型，去估计adjusted OR.

第二步：拟合带有协变量的Logistic模型 By fitting a binary logistic regression model we see there is no sex & treatment interaction on the unrestricted log odds scale, and the adjusted odds ratios for both treatment and sex are 9.

1
2

f <- glm(y ~ tx*sex, weights = freq, family = "binomial", data = d)
summary(f)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

Call:
glm(formula = y ~ tx * sex, family = "binomial", data = d, weights = freq)

Deviance Residuals: 
     1       2       3       4       5       6       7       8  
-26.33   26.33  -13.77   21.46  -21.46   13.77  -26.33   26.33  

Coefficients:
                Estimate Std. Error z value Pr(>|z|)    
(Intercept)   -2.197e+00  1.054e-01  -20.85   <2e-16 ***
txA            2.197e+00  1.229e-01   17.88   <2e-16 ***
sexfemale      2.197e+00  1.229e-01   17.88   <2e-16 ***
txA:sexfemale -1.093e-15  1.738e-01    0.00        1    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 5545.2  on 7  degrees of freedom
Residual deviance: 4072.9  on 4  degrees of freedom
AIC: 4080.9

Number of Fisher Scoring iterations: 5

And we calculated the Odds Ratio by exp(coef(f), and we get OR for treatment is 9:

1
2

(Intercept)           txA     sexfemale txA:sexfemale 
   0.1111111     8.9999997     8.9999997     1.0000000 

第三步：调整协变量不同水平上的响应比例，拟合带有协变量的Logistic模型

当我们调整模拟数据集为：在不同性别水平上，responder rate完全相同。此时Pooled marginal estimate变为9. 引入协变量sex与否不会影响推断。

代码为

1
2
3
4
5
6
7
8
9

d <- expand.grid(y=0:1, tx=c('A','B'),sex=c('male', 'female'))
# Order treatment levels to get OR > 1
d$tx <- factor(d$tx, c('B','A'))
d$freq <- c(500, 500, 900, 100, 500, 500, 900, 100)

# pooled marginal estimate of OR
f <- glm(y ~ tx, weights = freq, family = "binomial", data = d)
summary(f)
exp(coef(f))

1
2

(Intercept)         txA 
  0.1111111   8.9999997 

加入协变量sex校正以及输出

1
2
3
4

# adjusted OR
fm <- glm(y ~ tx*sex, weights = freq, family = "binomial", data = d)
summary(fm)
exp(coef(fm))

1
2

(Intercept)           txA     sexfemale txA:sexfemale 
  0.1111111     8.9999997     1.0000000     1.0000000 

这些计算表明，仅当分布发生变化，以致条件（condition）无关紧要时（例如，所有男性或所有女性都被排除在外），性别conditional OR 才等于边际 OR。

Conditional effects estimated by outcome regression

In the guidance document, FDA says > Sponsors should discuss with the relevant review divisions specific proposals in a protocol or statistical analysis plan containing nonlinear regression to estimate conditional treatment effects for the primary analysis. When estimating a conditional treatment effect through nonlinear regression, the model will generally not be exactly correct, and results can be difficult to interpret if the model is misspecified and treatment effects substantially differ across subgroups. Interpretability increases with the quality of model specification.

FDA建议申办者应与监管讨论方案或SAP中包含非线性回归的细节，以估计主要分析的conditional treatment effects。

当通过非线性回归估计conditional treatment effects时，模型一般不会完全正确。如果模型的设置不对，而且不同亚组的治疗效果差别很大，结果就很难解释。可解释性随着模型设置的质量而增加。

换句话说，FDA的观点是，调整协变量估计条件效应的回归（例如逻辑）模型的困难在于，没有理由说conditional odds ratio should be the same across subpopulations defined by the baseline covariates

Solution

Sponsors can perform covariate adjusted estimation and inference for an unconditional treatment effect (e.g., the odds ratio of 4.8 in Table 1) in the primary analysis of data from a randomized trial.

The method used should provide valid inference under approximately the same minimal statistical assumptions that would be needed for unadjusted estimation in a randomized trial.

If a novel method is proposed and statistical properties are unclear, the specific proposal should be discussed with the review division.

Covariate adjusted estimators of unconditional treatment effects that are robust to misspecification of regression models have been proposed for randomized clinical trials with - binary outcomes (Ge et al. 2011), - ordinal outcomes (Díaz et al. 2016), - time-to-event outcomes (Tangen and Koch 1999); (Lu and Tsiatis 2008).

Reference

• FDA Guidance - Adjusting for Covariates in Randomized Clinical Trials for Drugs and Biological Products

• Comments on FDA guidance ‘Adjusting for Covariates in Randomized Clinical Trials for Drugs and Biological Products’

• 一份很好的关于折叠性的解释：

  https://remlapmot.github.io/talk/

  文章：collap

• Ciolino, J. D., Martin, R. H., Zhao, W., Jauch, E. C., Hill, M. D., & Palesch, Y. Y. (2013). Covariate imbalance and adjustment for logistic regression analysis of clinical trial data. Journal of biopharmaceutical statistics, 23(6), 1383–1402. https://doi.org/10.1080/10543406.2013.834912

  文章：Covariate Imbalance and Adjustment for Logistic Regression Analysis of Clinical Trial Data

Appendix 1 - R code for FDA guidance Table 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

library(dplyr)

# simulate dataset
data_fda <- expand.grid(y=0:1, tx=c('New','Plb'),sex=c('male', 'female'))
# Order treatment levels to get OR > 1
data_fda$tx <- factor(data_fda$tx, c('Plb','New'))
data_fda$freq <- c(1000*0.2, 1000*0.8, 1000*(1-0.333), 1000*0.333, 
            1000*0.75, 1000*0.25, 1000*(1-0.04), 1000*0.04)

# overall odds ratio
f <- glm(y ~ tx, weights = freq, family = "binomial", data = data_fda)
summary(f)
exp(coef(f))

# subgroup odds ratio : male
data_fda_male <- data_fda %>%
  filter(sex=="male")
f_male <- glm(y ~ tx, weights = freq, family = "binomial", data = data_fda_male)
exp(coef(f_male))

# subgroup odds ratio : female
data_fda_female <- data_fda %>%
  filter(sex=="female")
f_female <- glm(y ~ tx, weights = freq, family = "binomial", data = data_fda_female)
exp(coef(f_female))

# add sex as a covariate to logistic model
f_cov <- glm(y ~ tx+sex, weights = freq, family = "binomial", data = data_fda)
summary(f_cov)
exp(coef(f_cov))

The result for # add sex as a covariate to logistic model is

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

> f_cov <- glm(y ~ tx+sex, weights = freq, family = "binomial", data = data_fda)
> summary(f_cov)

Call:
glm(formula = y ~ tx + sex, family = "binomial", data = data_fda, 
    weights = freq)

Deviance Residuals: 
      1        2        3        4        5        6        7        8  
-25.371   18.897  -23.244   27.061  -20.775   26.326   -8.849   16.049  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -0.69449    0.06341  -10.95   <2e-16 ***
txNew        2.08056    0.08948   23.25   <2e-16 ***
sexfemale   -2.48449    0.09164  -27.11   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 5207.5  on 7  degrees of freedom
Residual deviance: 3733.9  on 5  degrees of freedom
AIC: 3739.9

Number of Fisher Scoring iterations: 5

> exp(coef(f_cov))
(Intercept)       txNew   sexfemale 
 0.49933042  8.00894507  0.08336771