Parallel Gatekeeping - Alpha Propagation & General Multistage Gatekeeping Procedure

Posted on 2023-01-29 Edited on 2023-02-08 In Trial Design Word count in article: 1.9k Reading time ≈ 7 mins.

Alpha-Propagation

A key concept that has led to the development of novel methods for handling multiplicity problems of clinical trials is the concept of $\alpha$-propagation (Dmitrienko, Ajit C Tamhane, & Brian L Wiens, General multistage gatekeeping procedures, 2008).

If a null hypothesis (or endpoint) is tested at a level $\alpha$ (e.g., $\alpha\ = \ 0.05$) and its associated p-value is significant at this level, then this $\alpha$ is saved and is not lost. This alpha can then be recycled and propagated (or passed) to other null hypotheses or families of null hypotheses. This concept is used in methods such as the fallback, the graphical, and the more general chain methods for handing traditional multiplicity problems of clinical trials.

Alpha-Propagation rules

Suppose a problem with a parallel gatekeeper $F_1$

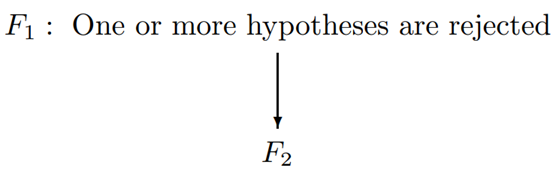
The $\alpha$-propagation rules can be described as

Two concepts that play a key role in the framework for constructing multistage parallel gatekeeping procedures: the error rate function of a multiple test and separable multiple tests.

Consider the problem of testing a single family of $n$ null hypotheses $H_1,\cdots,H_n$.

The index set $N=\left \{ 1,2,...,N \right \}$.

Error rate function - Definition

For any subset $I$ of the index set $N$, the error rate function of a multiple test is the maximum probability of making at least one type I error when testing the hypotheses $H_i, i\in I$, i.e.,

$$ e(I) = \sup_{H_{I}}{P\left\{ \bigcup_{i \in I}{\left( \text{Reject }H_{i} \right) \mid H_{I}} \right\}},\ \ I \subseteq N $$

The supremum ($\text{sup} P$) of the probability is taken over (or computed over the entire parameter space corresponding to the null hypotheses) the entire null space defined by

\[ H_{I} = \bigcap_{i \in I}^{}H_{i}. \]

Based on the definition above, we have:

(1)

$A_{1} = \varnothing$:

$e_{1}(\varnothing) = 0$, all null hypotheses are rejected in $F_{1}$; Here we have $\alpha_{2} = \alpha_{1} - e_{1}(\varnothing) = \alpha$.

Null hypotheses in $F_{2}$ are tested at full $\alpha$ level, where $\alpha$ is FWER (family-wised error rate).

注：这种情况即$F_1$中没有原假设被接受，即$F_1$中原假设都被拒绝

(2)

$A_{1} = N_{1}$:

$e_{1}\left( N_{1} \right) = \alpha$, no null hypotheses are rejected in $F_{1}$; Here we have $\alpha_{2} = \alpha_{1} - e_{1}\left( N_{1} \right) = 0$.

Null hypotheses in $F_{2}$ are not tested.

For an example, error rate function of Bonferroni procedure (reject any $H_i$ if $p_i \le \alpha /n$) is $e_{1}(I) = \frac{\alpha|I|}{k}$, where $|I|$ is the cardinality^[a] of set $I$.

Error rate function - Monotonicity

In addition, it is natural to require that the error rate function be monotone, i.e., \[ e(I)\le e(J) \text{ , if } I \subseteq J. \] If the monotonicity condition is not satisﬁed, one can easily enforce monotonicity by using the following upper bound $e^{\ast}(I)$ in place of the original error rate function $e(I)$: \[ e^{\ast}(I)=\max_{I' \subseteq I}e(I'). \] It is easy to see that $e^{\ast}(I)$ is a monotone error rate function.

显然，在$I \subseteq J$下，$e^{\ast}(I) \le e^{\ast}(J)$.

For any MTP, if an exact computable expression for $e(I)$ is available then we set $e^{\ast}(I)=e(I)$; otherwise we will treat $e^{\ast}(I)$ itself as the error rate function and state all the formulas in terms of $e^{\ast}(I)$.

Separable procedures

A multiple test meets the separability condition (and is termed separable) if its error rate function is strictly less than (separates from) $\alpha$ unless all hypotheses are true, i.e., \[ e(I) < \alpha \text{ , for all } I \subset N. \] In another word, say Procedure 1 is separable if $e_{1}(I) < \alpha$ provided $I$ is a proper subset^[b] of $N_{1}$.

That is, if a separable procedure is used in $F_{1}$, a fraction of $\alpha$ can be carried over to $F_{2}$ if one or more null hypotheses are rejected in $F_{1}$.

The Bonferroni test clearly satisﬁes this condition since $e(I) < \alpha$ for any index set $I$ with less than $n$ elements.

Table - Bonferroni versus Holm with the separable property; Note that $N_{1} = \{ 1,2,3\}$.

For Holm step-down MTP, the Holm MTP incorrectly rejects any true hypothesis with probability $\alpha$ and hence is not separable.

But why?

Recall the algorithm of Holm (from Wiki):

Consider the following test: \[ H_i:\mu_i=0 \ \ \text{v.s.} \ \ H_i^{'}:\mu_i \gt 0 \ \ (1 \le i \le n) \] Suppose

$\mu_j=0$ for some $j$
$ +$ for $i \ne j$

Then p-values for $i$ computed as $p_i \rightarrow 0$ for all $i \ne j$, and $p_j$ will be the largest p-value $p_{(n)}$. Based on the algorithm above, this MTP will proceed until testing "is $p_j=p_{(n)}\lt \alpha \text{?}$". Therefore, $p_j$ will be compared with $\alpha$ and $H_j$ will be rejected with probability $\alpha$.

Separability procedures

Most popular procedures (Holm, fallback, Hochberg and Hommel procedures) do not satisfy the separability condition (Dmitrienko, Ajit C Tamhane, & Brian L Wiens, General multistage gatekeeping procedures, 2008).

Truncated procedures

Truncated procedure is based on a convex combination^[c] between a multiple procedure and Bonferroni procedure. Truncated procedure is separable.

Truncated p-value-based procedures: Truncated Holm, fallback and Hochberg procedures.
Truncated parametric procedures: Truncated step-down Dunnett procedure.

Refer to the paper General Multistage Gatekeeping Procedures (Dmitrienko, Ajit C Tamhane, & Brian L Wiens, General multistage gatekeeping procedures, 2008) for more details of truncated procedures.

Truncated Holm will be described in appendix.

Gatekeeping procedures

Wide variety of parallel gatekeeping procedures can be built based on these truncated procedures.

Algorithm of general multistage gatekeeping procedure

The algorithm is developed based on the $\alpha$-Propagation rules.

Proposition

The 2-stage gatekeeping procedure controls the FWER at the $\alpha$ level.

The simple two-stage procedure provides useful insights into the nature of gatekeeping inferences. It is important to note that any FWER-controlling MTP can be used at the second stage of the 2-stage gatekeeping procedure. Therefore, one can construct gatekeeping procedures with an arbitrary number of stages by a recursive application of the two-stage procedure.

Since a serial gatekeeper can be expressed as a series of single-hypothesis families, multistage gatekeeping procedures obtained via the recursive algorithm can have a very flexible structure that combines serial gatekeepers and parallel gatekeepers.

Characteristics to define the multistage gatekeeping procedure

$m \geq 2$ families;

$F_{i} = \{ H_{i1},\ldots,H_{im}\}$ for $1 \leq i \leq m$;

$N_{i} = \{ 1,\ldots,n_{i}\}$ and $A_{i} \subseteq N_{i}$ be the index set corresponding to the accepted hypotheses in $F_{i}$;

The algorithm for applying the procedure is:

Remarks

If all hypotheses are rejected at the $i$-th stage ($1 \leq i \leq m - 1$), then $A_{i} = \varnothing$ and $\alpha_{i + 1} = \alpha_{i}$. Thus full $\alpha_{i}$ is carried over to the next stage.
At the final stage, any FWER controlling multiple testing procedure may be used, but a truncated multiple testing procedure should not be used since it is less powerful than its untruncated version.

^[a] In mathematics, the cardinality of a set is a measure of the "number of elements of the set". ^[b] A proper subset (真子集) of a set A is a subset of A that is not equal to A. In other words, if B is a proper subset of A, then all elements of B are in A but A contains at least one element that is not in B. For example, if A={1,3,5} then B={1,5} is a proper subset of A. The set C={1,3,5} is a subset of A, but it is not a proper subset of A since C=A. The set D={1,4} is not even a subset of A, since 4 is not an element of A. ^[c] 在凸幾何（英語：Context geometry）領域，凸組合（英語：convex combination）指點的線性組合，要求所有係數都非負且和為 1。此處的「點」可以是仿射空間中的任何點，包括向量和純量。

Example: EPHESUS trial

This trial (Bertram Pitt, et al., 2001) was conducted to assess the effects of eplerenone on morbidity and mortality in patients with severe heart failure. In this clinical trial example, we will consider two families of endpoints:

Two primary endpoints:
- all-cause mortality (Endpoint P1, with hypothesis^[d] $H_{11}$)
- cardiovascular mortality + cardiovascular hospitalization (Endpoint P2).
Two major secondary endpoints:
- cardiovascular mortality (Endpoint S1)
- all-cause mortality + all-cause hospitalization (Endpoint S2).

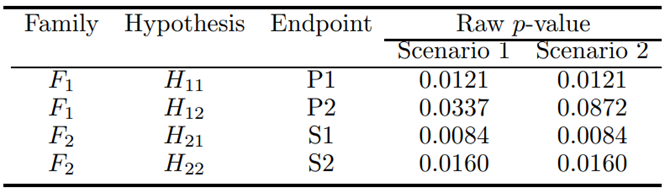
The family of primary endpoints serves as a parallel gatekeeper for the family of secondary endpoints. The hypotheses are equally weighted within each family and the pre-specified FWER is $\alpha = 0.05$. Table 10 displays two sets of two-sided p-values for the four endpoints that will be used in this example (note that these p-values are used here for illustration only).

Table - Two-sided p-values in the cardiovascular clinical trial example.

A two-stage parallel gatekeeping procedure will be set up as follows:

The hypotheses in $F_1$ and $F_2$ will be tested using the truncated and regular Holm tests, respectively.

The truncated Holm test is carried out using four values of the truncation parameter ($\gamma =$ 0, 0.25, 0.5 and 0.75) to evaluate the impact of this parameter on the outcomes of the four analyses.

Scenario 1

Let $\gamma = 0.25$. The hypotheses $H_{11}$ and $H_{12}$ are tested using the truncated Holm test at $\alpha_{1} = \alpha = \ 0.05$. The smaller p-value, $p_{11} = 0.0121$, is less than

\[ \left\lbrack \frac{\gamma}{2} + \frac{1 - \gamma}{2} \right\rbrack\alpha = \frac{\alpha}{2} = 0.025 \]

And thus $H_{11}$ is rejected.

Further, $p_{12} = 0.0337$, is compared to

\[ \left\lbrack \frac{\gamma}{2} + \frac{1 - \gamma}{2} \right\rbrack\alpha = \frac{5\alpha}{8} = 0.03125. \]

The corresponding hypothesis cannot be rejected.

To find the fraction of $\alpha$ that can be carried over to the hypotheses in $F_2$, note that the set of retained hypotheses in $F_1$ includes only one hypothesis. Thus,

\[ \alpha_{2} = \alpha_{1} - e_{1}\left( A_{1} \right) = \alpha - \left\lbrack \gamma + \frac{(1 - \gamma) \mid A_{1} \mid}{n} \right\rbrack\alpha = \frac{3\alpha}{8} = 0.01875, \]

Where $\mid A_1 \mid = 1$ and $n = 2$.

Applying the regular Holm test in $F_2$ at $\alpha_2$, it is easy to verify that $H_{21}$ and $H_{22}$ are rejected at level $\alpha_2$.

^[d] Assume no treatment effect between treatment groups.

Appendix - Truncated Holm

Screenshot from A. Dmitrienko, A. C. Tamhane and B. L. Wiens: Multistage Gatekeeping Procedures