To add details for Section 3.2 in the paper A recycling framework for the construction of Bonferroni-based multiple tests.

Rejection algorithm for a recycling MTP in terms of the default graph

Note

• In Burman's work, test mass refers to (parts of) the nominal level \(\alpha\) at which the family-wise error rate is controlled. Briefly, test mass is split between different null hypotheses, and whenever a null hypothesis is rejected, the part of allocated to it may be recycled to the testing of other hypotheses.

• A sequence is simply defined as a sequence, of any length, of hypotheses in the family \(S\) considered.

  

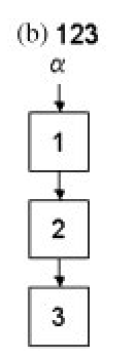
• A collection \(c\) consists of a number \(m\) of sequences, \(s_1,..., s_m\), with associated positive weights \(w_1,...,w_m\). The sum of the weights is required to be 1. A collection may be displayed as a default graph. A number of collections may be combined in sequence or in parallel to form a new collection.

• In several of the examples in Burman's work, he displayed the same MTP by two (or more) graphical representations. Every recycling MTP can be displayed by something referred to as a default graph. Such a graph splits the test mass into several parts (not necessarily of equal size), each allocated to a fixed-sequence of hypotheses.

  

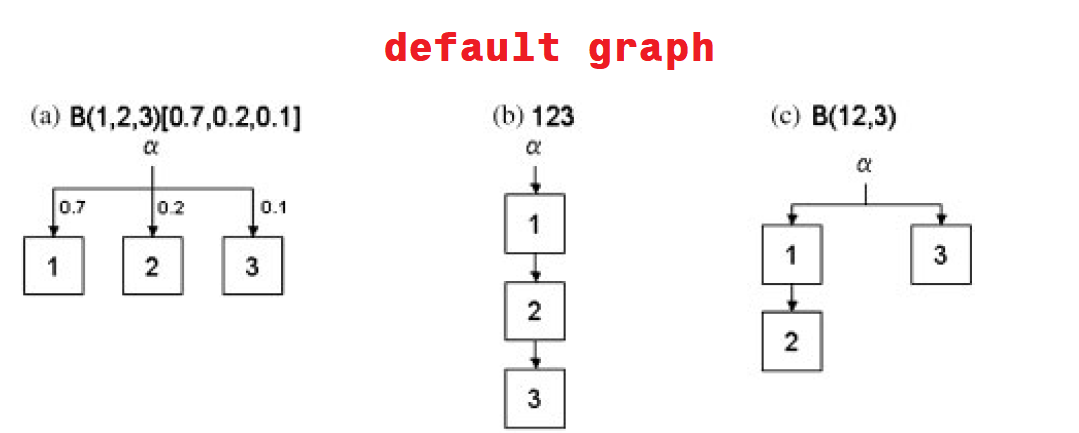
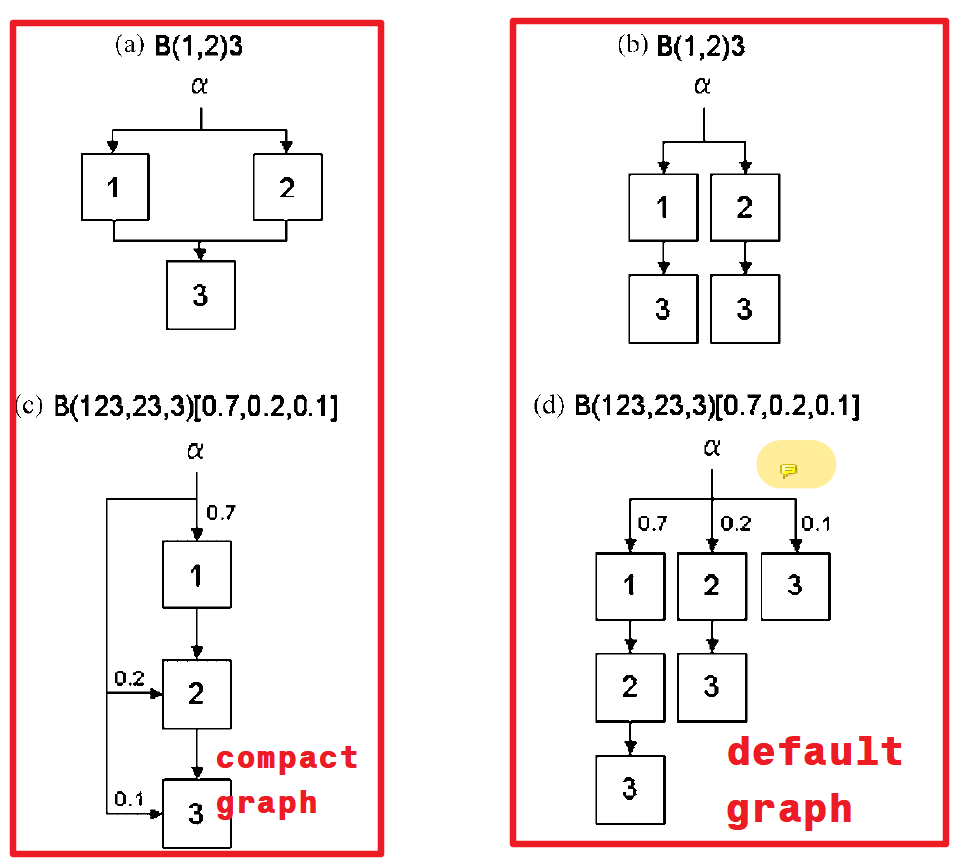
• Test mass \(\alpha_k(A)\) will represent the available test mass for hypothesis \(k\) if the hypotheses in \(A \subset S\) are rejected.【注：比如，算法的第1步中，\(\alpha_i(A=\emptyset)\)可计算为每个假设\(H_i\)分配到的初始权重\(\omega_i\)乘上总的\(\alpha\)，即\(\alpha_i(\emptyset)=\omega_i \times \alpha\)】

如果假设检验\(k\)不在step 1中被拒绝的检验中，也就是\(k \in S \setminus A_1\),那么\(k\)可能在step 2中被拒绝。因为从default graph中删除了所有与\(A_1\)相关联的boxes后，可能\(k\)就成了若干个sequences的初始节点（或者说假设假设检验），因此有\(\alpha_k(A_1) \ge \alpha_k(\emptyset)\).更一般的，recycling of test mass反应在如下的\(\alpha_k(A)\)单调性中（作为集合\(A\)）的函数： \[ \text{if} \ \ A_{\ast} \subset A_{\ast \ast} \subset S \text{ and } k \in S \setminus A_{\ast \ast},\text{ then } \alpha_k{(A_{\ast \ast})}\ge \alpha_k{(A_\ast)} \] In the next paragraph, we will give a short direct proof of the important fact that the MTP defined through Algorithm 1 strongly controls its type-I FWER to be \(\le \alpha\). This proof does not refer to the closed test procedure.

Proof

Let \(T\) denote the unknown set of true hypotheses in \(S\).

Let \(E_1\) be the event that Algorithm 1 rejects at least one hypothesis in \(T\). (拒绝\(T\)中的假设检验会犯Type I error)

The problem is thus to proof \[ \text{Pr}(E_1)\le \alpha. \]

The whole proof is done by showing \(E_2\) occurs whenever \(E_1\) occurs

(Part-1) \[ E_2=\bigcup_{k \in T} \left [ p_k \le \alpha_k(S\setminus T) \right ] , \]

and then

(Part-2) \[ \text{Pr}(E_2) \le \alpha. \]

以下用中文阐述证明思路，英文原文参考论文。

(Part-1) 表示的是，\(k\)是真实原假设集合\(T\)中的一个元素，Type I error只会发生在“拒真”的情况下，也就是拒绝\(T\)中的任意一个元素。则\(T\)的补集\(T^C=S \setminus T\)包含的都是非真原假设，拒绝\(T^C\)中的假设不会导致Type I error膨胀。式子\(p_k \le \alpha_k(S\setminus T)\)表示的是，在拒绝了\(T^C\)后，假设检验只剩下\(T\)，在此test mass上，\(k\)的p值小于给定test mass，即\(k\)显著。则事件\(E_2\)定义为，拒绝掉\(T^C\)后，至少有一个\(k \in T\)显著。显然，事件\(E_2\)是Type I error inflation的根本来源；

(Part-2) 表示的是，这种Type I error发生概率需要控制在\(\le \alpha\)。

假设\(E_1\)发生了，即按照Algorithm 1，MTP中至少拒绝了1个集合\(T\)中的真实原假设。假设拒绝发生在第\(i\)步(\(i \ge 1\) but why?)，则当前步骤\(i\)下，Rejection Set \(R_i \subset S \setminus A_{i-1}\)至少包含1个假设\(k \in T\)。

对于第\(i\)步，根据Algorithm 1，需\(p_k \le \alpha_k(A_{i-1})\)。由于在第\(i\)步之前，没有\(T\)里的假设被拒绝，即\(A_{i-1} \subset S \setminus T\)，所以根据集合\(A\)的函数\(\alpha_k(A)\)的单调性，可以得出 \[ \alpha_k(A_{i-1}) \le \alpha_k(S \setminus T). \] 即，当前步骤中存在p值，使得\(p_k \le \alpha_k(A_{i-1}) \le \alpha_k(S \setminus T), \ \ k \in T\)，即证(Part-1)。

由于\(\text{Pr}(E_1) \le \text{Pr}(E_2)\)，根据Boole’s inequality ^[a]，以及\(\text{Pr}(p_k \le u) \le u \ \ \text{if } u \in [0,1]\)和\(k \in T\)，有 \[ \begin{align*} \text{Pr}(E_2) &= \text{Pr}(E_2) \\\\ &=\text{Pr}(\bigcup_{k \in T} \left [ p_k \le \alpha_k(S\setminus T) \right ]) \\\\ &\le \sum_{k \in T}(\text{Pr}[p_k \le \alpha_k(S\setminus T)]) \\\\ &\le \sum_{k \in T}(\alpha_k(S\setminus T)) \end{align*} \] 此外，每一个\(\alpha_k(S \setminus T)\) （其中\(k \in T\)）都基于reduced sequences from the default graph，它们只包含\(T\)中真实的原假设。所以他们在\(k \in T\)上的综合至多等于\(\alpha\)乘上default graph中初始sequences的权重和\(w_i\)。所以证得(Part-2)。

^[a] In probability theory, Boole's inequality, also known as the union bound, says that for any finite or countable set of events, the probability that at least one of the events happens is no greater than the sum of the probabilities of the individual events. This inequality provides an upper bound on the probability of occurrence of at least one of a countable number of events in terms of the individual probabilities of the events. Wiki