An Intuitive Explanation for the Interaction of Factors in a Multiple Regression

Here is an excellent answer I have read when I was in university for the interpretation of interactions in linear model.

Question

Given:

y = A + B

y = A + B + A*B

If both models are "statistically significant", which one should I prefer and why? What's the appropriate interpretation of the interaction?

Answer

It may sound a bit counter-intuitive, but what helps me the most in getting my bearings on this issue is the linear algebra. In a linear model with interactions, and avoiding matrices, the mathematical expression for two regressors is:

\[ \hat Y=\hat\beta_0+\hat\beta_1\,X_1+\hat\beta_2\,X_2+\hat\beta_3\, \color{blue}{X_1*X_2} \]

So imagine the easy scenario:

• Variable \(X_2\) is categorical with factors \(A\) and \(B\). For instance it could be the variable gender with values M and F coded as 0 and 1.

• Variable \(X_1\) is a continuous measurement.

For M, \((X_2=0), \color{blue}{X_1*X_2 = X_1\,*\,0 =0}\) for all M observations.

We end up with \(\hat Y=\hat\beta_0+\hat\beta_1\,X_1\), with the intercept being \(\hat\beta_0\) and the slope \(\hat\beta_1\).

For F, \((X_2=1), \color{blue}{X_1*X_2 = X_1\,*\,1 =X_1}\).

We end up with \(\hat Y=\hat\beta_0+\hat\beta_1\,X_1+\hat\beta_2\,\color{blue}{1}+\hat\beta_3\, \color{blue}{X_1}\) with intercept \(\hat\beta_0+\hat\beta_2\) and slope \(\hat\beta_1+\hat\beta_3\).

So notice that for each factor, and due to the interaction, you wind up with different intercepts and different slopes.

If there was no interaction, the model would be:

\[ \hat Y=\hat\beta_0+\hat\beta_1\,X_1+\hat\beta_2\,X_2 \]

And we would obtain one single slope for both M and F, \(\hat\beta_1\) and two different intercepts: \(\hat\beta_0\) for M and \(\hat\beta_0+\hat\beta_2\) for F.

So the presence of an interaction changes the relationship of the continuous variable \(X_1\) with the predicted values (the slope).

This would be the difference in the plotted curves with M and F color coded:

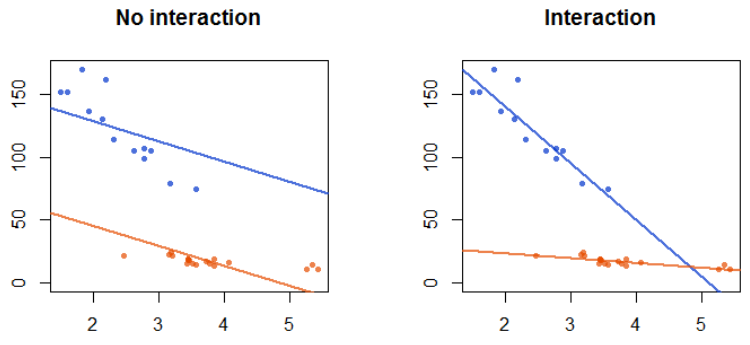
Antoni Parellada, What is an intuitive explanation for the interaction of factors in a multiple regression?, URL (version: 2016-03-22): https://stats.stackexchange.com/q/202919 ^{*Content contributed from 2011-04-08 up to but not including 2018-05-02 (UTC) is distributed under the terms of CC BY-SA 3.0}