Linear Model in SAS (2.1) - the Design Matrix Is of Less Than Full Rank !
There are three ways to find a solution for linear model parameters when the design matrix is of less than full rank. 这篇是Linear Model in SAS (2)中Estimable Functions的先决知识点.本文为辅助材料,整理自JH的讲义。
Introduction

其中第2点也是如下博文采用的方法:
Linear Model in SAS (2) - Hypothesis Testing and Estimable Functions
Reducing the Model to One of Full Rank

Example: (One-way ANOVA with 2 groups)

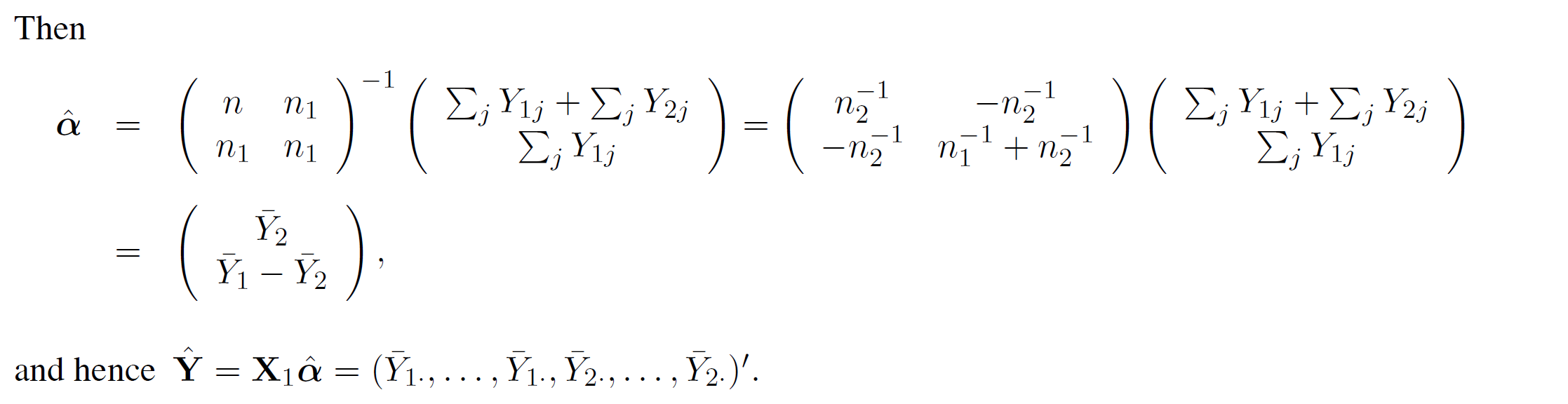
Finding a Generalized Inverse \((X'X)^-\)

Theorem
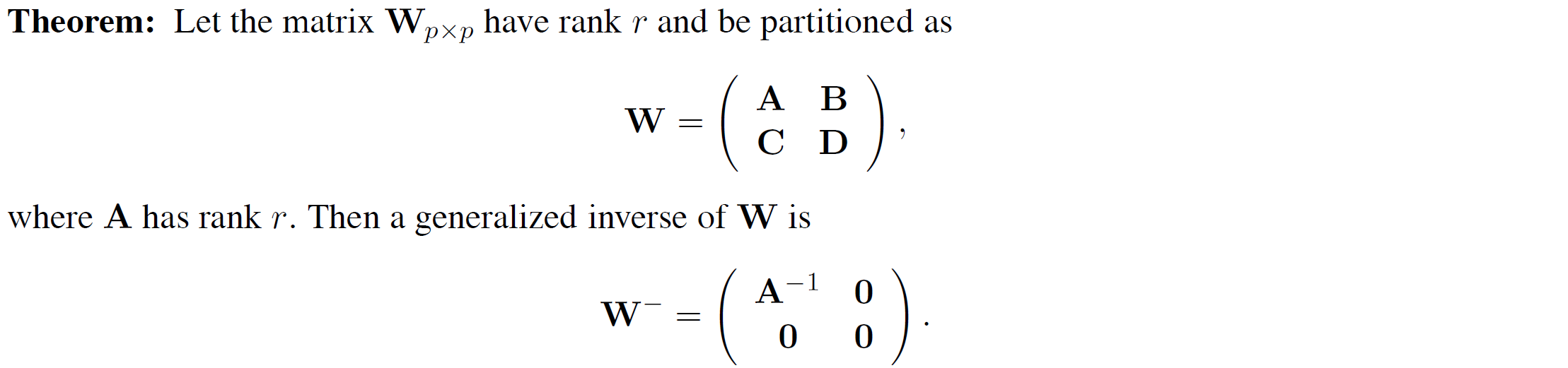
Example: (One-way ANOVA with 2 groups, continued)
We have
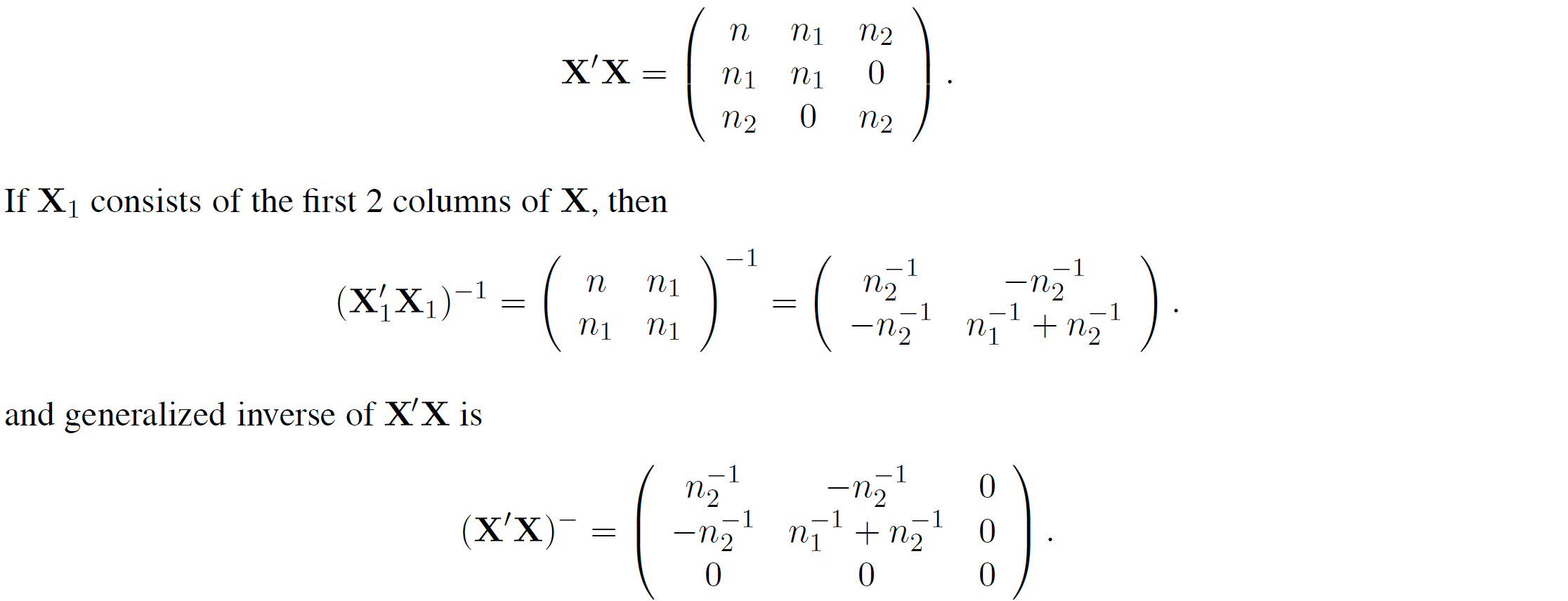
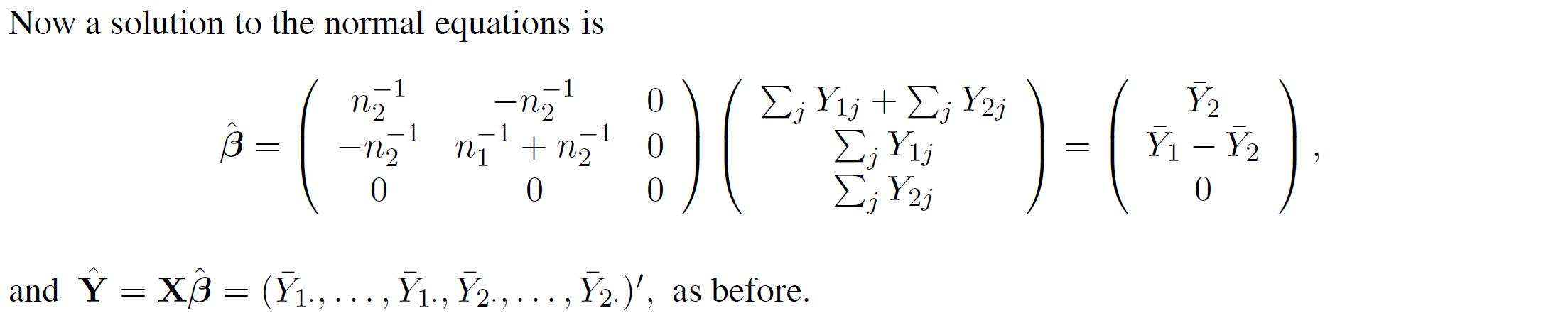
Imposing Identifiability Constraints
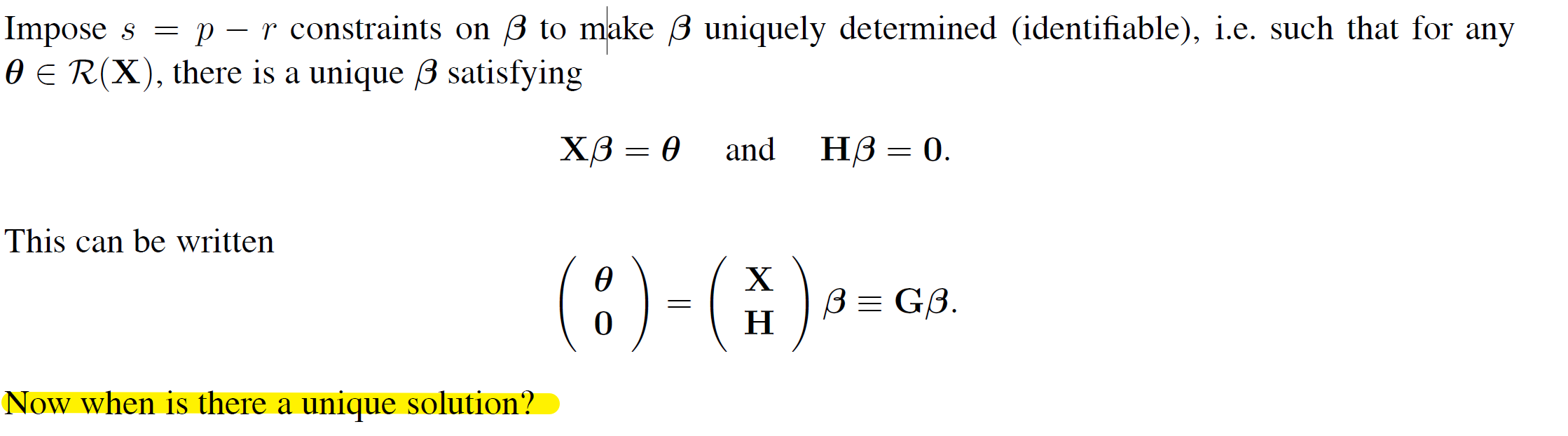
Theorem
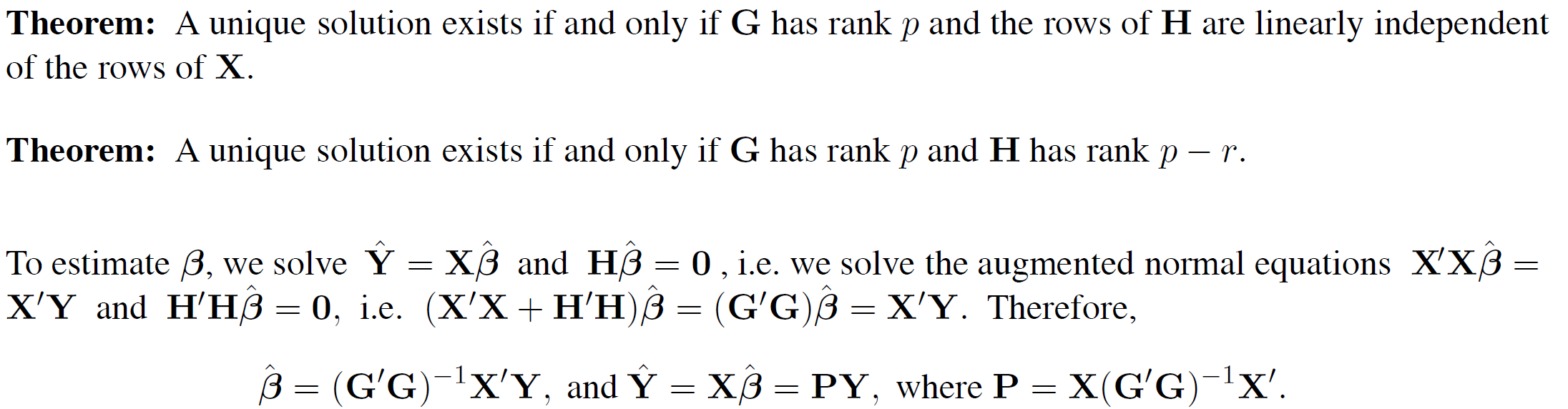
Example: (One-way ANOVA with 2 groups, cont.)
Set \(\alpha_1+\alpha_2=0\), i.e.

Reference
Full lecture note of this topic can be found in
Full course material could be found in
An overview of the topic for this course
Chapter 1: Introduction
Chapter 2: Review of linear algebra and matrices
Chapter 3: Random vectors
Chapter 4: The multivariate normal distribution and distributions of quadratic forms
Chapter 5: Least squares estimation
Chapter 6: Properties of least squares estimates
Chapter 7: Design matrices of less than full rank
Chapter 8: Orthogonal structure in the design matrix
Chapter 9: Generalized least squares
Chapter 10: Estimable functions
Chapter 11: Hypothesis testing